mathématiques

Il s'agit ici de mettre les élèves dans un bain visuel et de les faire réagir.
Il n'y a pas vraiment un énoncé mais un document support (voir ci-dessous), qui peut être un fil conducteur pour le professeur et éventuellement un document-trace à distribuer, aux élèves, en fin de séance.
Cette activité peut se dérouler :

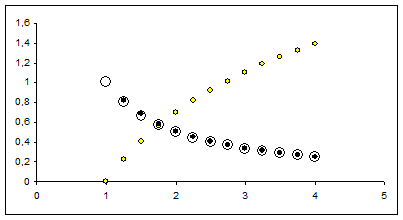
Le professeur présente  la représentation graphique (C_f)  d'une fonction f  positive sur l'intervalle [1 ; 8] et l'objectif qui est d'approcher l'aire du domaine compris entre la courbe (C_f), l'axe des abscisses et les droites d'équation x = 1 et x = 8.

Après discussion avec les élèves sur différentes stratégies possibles, on décide de partager le segment [1 ; 8] en 28 segments de longueur 0,25 et  on approche le domaine par une suite de trapèzes.
Sur le segment [1 ; 8], on construit des points A_k(x_k ; 0) où les x_k sont en progression arithmétique de premier terme x₀ = 1 et de raison 0,25. On note a_k les aires cumulés des k premiers trapèzes k variant de 0 à 28.

Une fois cette situation présentée, les élèves utilisent leurs connaissances sur les tableurs pour créer une feuille automatisée de calcul donnant les différentes valeurs des x_k et les valeurs correspondantes des a_k. Ils représentent ensuite le nuage de points M_k(x_k ; y_k).

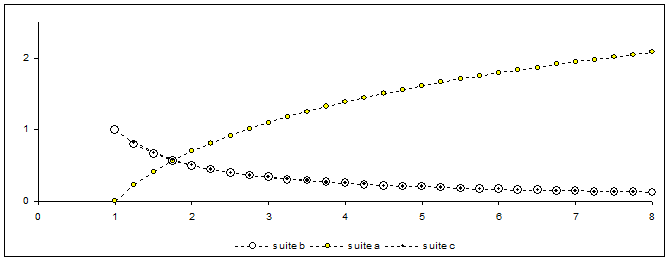
Le professeur reprend la main pour avancer l'idée que les points M_k pourraient être considérés comme points d'une même courbe représentative d'une certaine fonction nommée F. Pour tenter de mieux connaître F, on décide d'approcher sa dérivée en associant  à chaque nombre x_k le coefficient c_k de la droite (M_k-1M_k+1).

A nouveau, les élèves utilisent le tableur pour calculer les différents termes de la suite c_k (1 < k < 28) puis pour construire le nouveau nuage de points de coordonnées A_k(x_k ; c_k). A partir de ce résultat, commence la troisième phase de l'activité.

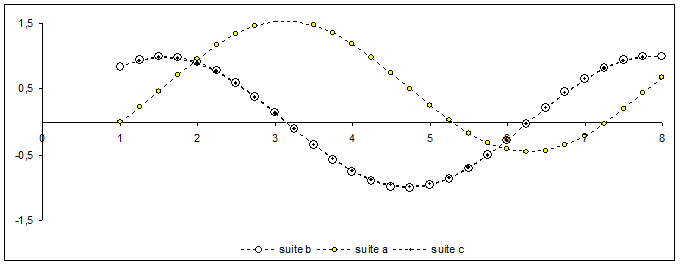
Il s'agit maintenant de laisser complètement la parole aux élèves pour explorer et commenter le résultat graphique. La conjecture  « on dirait que F' = f  » pourra être énoncée et surtout testée en faisant des essais avec différentes fonctions f.