espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques
Introduction au calcul intégral
mis à jour le 26/09/2007
mots clés : intégral, rectangle, trapèze, primitive, géoplanw
Méthode des rectangles
Objectifs :
Introduction de la notion d' intégrale par la méthode des rectangles.
Etude de deux suites convergentes.
Utilisation du logiciel Géoplanw par le professeur présentant les résultats de cette activité en classe, à l'aide d'un rétroprojecteur ou d'un vidéoprojecteur.
Utilisation par des élèves, dans une salle multimédia, du fichier "integrec.g2w" installé préalablement par le professeur. Les élèves peuvent retouver les résultats de l'activité, modifier la fonction, et changer les bornes d'intégration.
Etude de deux suites convergentes.
Utilisation du logiciel Géoplanw par le professeur présentant les résultats de cette activité en classe, à l'aide d'un rétroprojecteur ou d'un vidéoprojecteur.
Utilisation par des élèves, dans une salle multimédia, du fichier "integrec.g2w" installé préalablement par le professeur. Les élèves peuvent retouver les résultats de l'activité, modifier la fonction, et changer les bornes d'intégration.
Activité:
Démontrer par récurrence que :
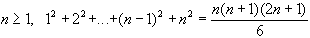
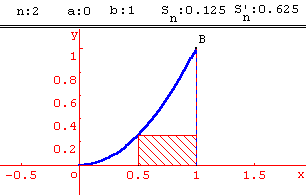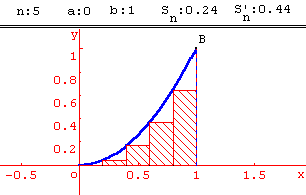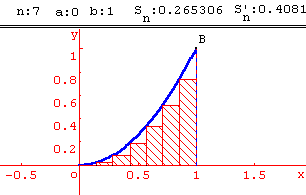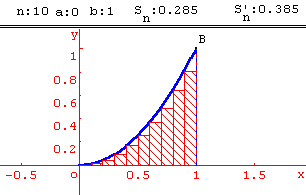
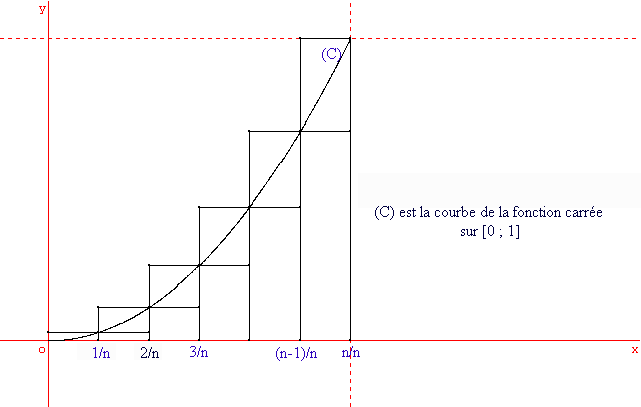
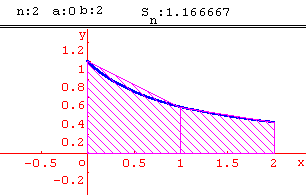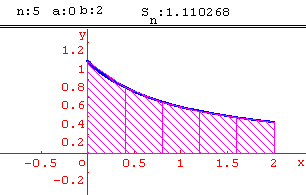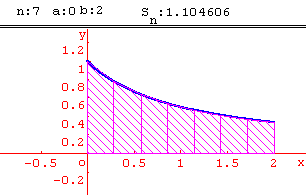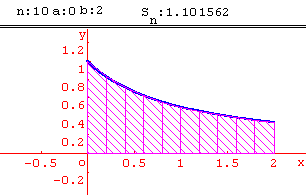
On se propose de calculer l'aire A de la partie du plan comprise entre l'axe des abscisses, la courbe ( C) et les droites d'équations x = 0 et x = 1 (l'unité d'aire est l'aire du carré construit sur les vecteurs de base).
Pour cela, on subdivise l'intervalle [0 ; 1] en n intervalles :
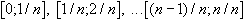
On appelle un la somme des aires des " petits " rectangles ainsi construits et vn la somme des aires des " grands " rectangles " et on admettra que :
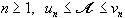
1. Calculer u6 et v6 et en déduire un encadrement de A.
2. Vérifier que :
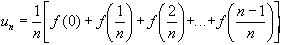
3. Démontrer que :
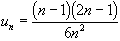
4. Calculer :
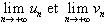
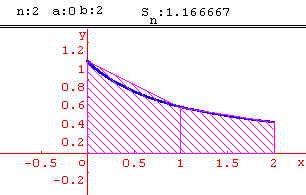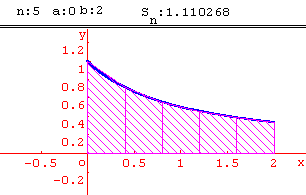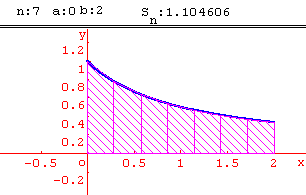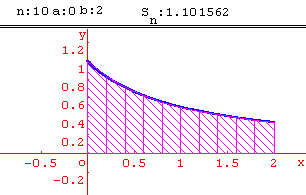
Méthode des trapèzes
Objectifs :
Calcul approché d' intégrales par la méthode des trapèzes.
Utilisation du logiciel Géoplanw par le professeur en classe, à l'aide d'un rétroprojecteur ou d'un vidéoprojecteur.
Utilisation du fichier "integtra.g2w" par des élèves, dans une salle multimédia. Les élèves peuvent tester différentes fonctions, en changeant les bornes d'intégration.
Activité:
En utilisant la fonction inverse, calculer par la méthode des trapèzes une valeur approchée de ln 2. On pourra utiliser une subdivision de l'intervalle [1; 2] en 10 intervalles de même amplitude.
Intégrales et primitives - Fonction logarithme népérien
Objectifs :
Lien entre calcul d'aire, intégrale et primitive.
Introduction de la fonction logarithme népérien.
Utilisation du logiciel Géoplanw par le professeur en classe, à l'aide d'un rétroprojecteur ou d'un vidéoprojecteur.
Utilisation par des élèves dans une salle multimédia : les élèves utilisent le fichier "primitiv.g2w" installé par le professeur et testent différentes fonctions f, afin de faire des conjectures sur la fonction F. L'on peut essayer successivement f(x) = 1, f(x) = x, f(x) = cos x ...
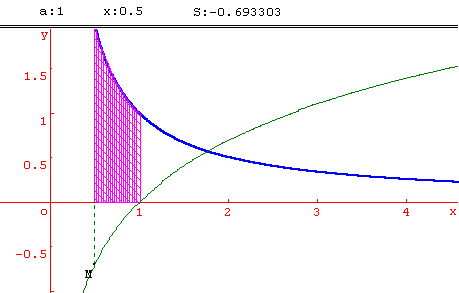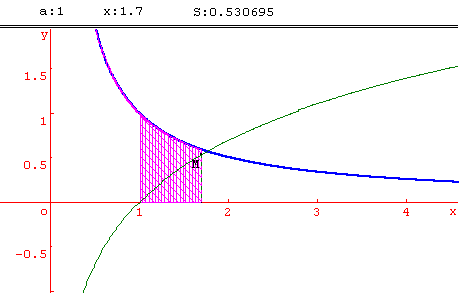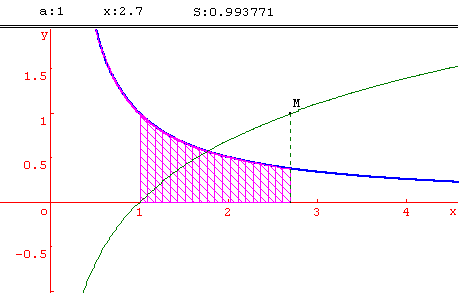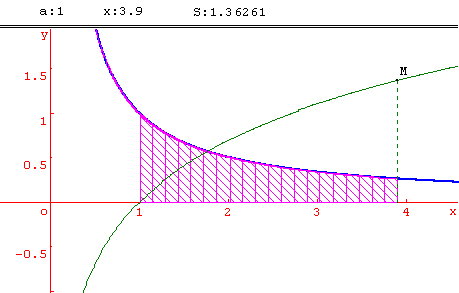
Commentaires:
f étant une fonction dérivable et strictement monotone sur un intervalle [a; b], x désignant un réel de l'intervalle [a; b], on note F(x) l'aire de la partie du plan limitée par l'axe des abscisses, la courbe de f et les droites d'équations X = a et X = x.
Le fichier Géoplanw permet la visualisation de la fonction F, en affichant x et F(x), et en construisant la courbe de F. Le point M(x; f(x)) se déplace sur la courbe de F en pilotant x au clavier. Le calcul d'aire effectué est un calcul approché, utilisant la méthode des trapèzes (20 trapèzes construits). Il convient donc de se limiter à un intervalle [a ;x] pas trop étendu.
L'on peut modifier la fonction f , ainsi que la borne a. En prenant f(x) = 1/x et a = 1, l'on introduit la fonction ln.
Il n'est pas nécessaire que la fonction f soit strictement monotone pour visualiser la courbe d'une primitive de f. L'on peut, par exemple, prendre f(x) = cos(x) et vérifier que la primitive de f qui s'annule en 0 est définie par F(x) = sin(x).
Le chargement du fichier "primitiv.g2w" est assez long !
Louis Gallard
information(s) pédagogique(s)
niveau : Terminale S
type pédagogique : exercice
public visé : enseignant, élève
contexte d'usage : non précisé
référence aux programmes :
documents complémentaires
| Les fichiers associés |
| Méthode des rectangles Méthode des trapèzes Primitives |
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA