espace pédagogique > disciplines du second degré > mathématiques - sciences > enseignement
Nombre de barreaux sur une balustrade
mis à jour le 10/03/2021
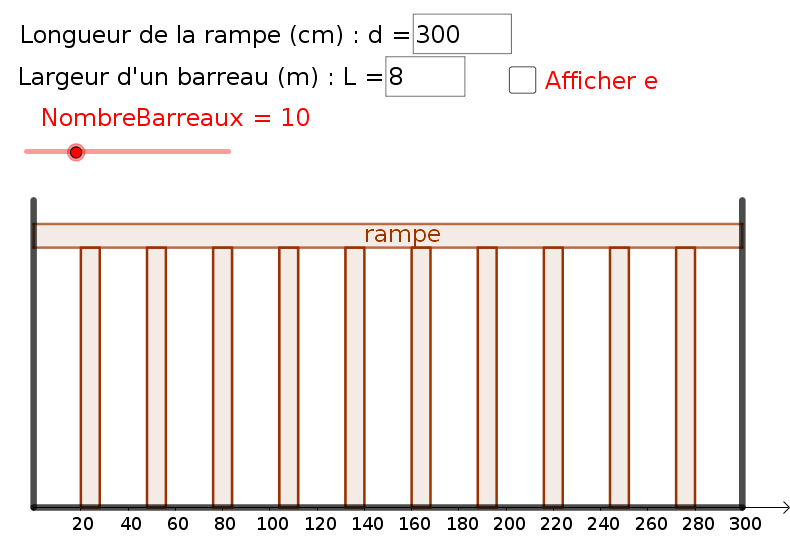
Comment déterminer le nombre minimal de barreaux à installer sous la rampe d'une balustrade pour qu'un enfant ne puisse pas y passer la tête ? À partir d'une configuration donnée (longueur de la rampe, largeur des barreaux et nombre de barreaux), pour laquelle les élèves calculent l'espace entre 2 barreaux, on leur propose ensuite de construire et tester :
- Un programme Python qui calcule l'espace entre deux barreaux pour un nombre de barreaux données
- Un programme Python qui recherche le nombre de barreaux pour que l'espace ne dépasse pas 11 cm (norme de sécurité) en augmentant progressivement le nombre de barreaux
- Un programme capable de faire la même chose avec n'importe quelles longueurs de rampe et largeurs de barreaux
style="text-align: center;">
 Deux "coups de pouce" sont prévus pour aider les élèves à surmonter certaines difficultés.
Deux "coups de pouce" sont prévus pour aider les élèves à surmonter certaines difficultés.mots clés : mathématiques, python
Déroulement de la séquence :
Une mise en commun peut-être faite à l'issue de la question 2).
Les élèves travaillent en autonomie sur poste informatique, des coups de pouce (à la question 3) et à la question 6)) avec des scripts pouvant être testés leur permettent d'avancer à leur rythme.
Les plus rapides pourront travailler jusqu'à la question 7) avec la nécessité d'introduire les variables d et L.
Points de blocage (aides à apporter aux élèves) :
- le nombre d’espaces entre les n barreaux est n + 1 (la simulation informatique doit les amener à se questionner)
- Mise en équation e = (300 – n*8)/(n+1) (le coup de pouce 1 amène l'élève à réfléchir sur cette expression)
- L’utilisation de la répétition non bornée WHILE (les élèves disposent du MiniMemo Python simplifié en ressource). Le coup de pouce 2 (possibilité de tester les scripts) fait ressortir la différence avec l'instruction conditionnelle et l'importance d'initialiser n et e avant la boucle.
Objectifs de l'activité :
- Résolution d'une situation en faisant une recherche par balayage avec Python
- Utilisation d'une boucle While dans Python
Connaissances et savoir-faire préalables :
- En maths : Mise en équation
- En Python : types de variables, gestion des entrées-sorties, opérations de base, opérateur de comparaison.
Compétences visées :
- S'approprier
- Analyser raisonner
- Réaliser
- Valider
information(s) pédagogique(s)
niveau : tous niveaux, 2nde professionnelle, bac pro
type pédagogique : activité de découverte, activité de recherche, exercice
public visé : élève, enseignant
contexte d'usage : classe, salle multimedia
référence aux programmes : Analyse - algèbre
Algorithmique et programmation
fichier joint
information(s) technique(s) : Fichier zip à décompresser contenant :
- La fiche pédagogique de l'activité
- Le support à compléter pour les élèves avec les 2 coups de pouce et le corrigé
- Les deux scripts Python
- Le fichier GeoGebra pour validation
- Le minimémo Python pour les élèves.
format : #saisir ; taille : 315 ko ; durée : 1 h
mathématiques - sciences - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA
