mathématiques
s'identifier
portail personnel ETNA
espace pédagogique > disciplines du second degré > mathématiques > enseignement > activités pédagogiques
Aires du parallélogramme, du tiangle et du trapèze
mis à jour le 20/01/2007
Les fichiers cabri proposés ne sont que des imagiciels qui peuvent être utilisés en classe pour animer des séquences de travail sur les aires, la recherche étant faite préalablement par les élèves.
Ils peuvent permettre de faire une synthèse de cette recherche, et montrer ainsi à chaque élève d'autres solutions que celle qu'il a trouvée.
Les exemples proposés pour déterminer l'aire du trapèze peuvent être utilisés dans les classes ultérieures comme exemples de calcul littéral.
mots clés : Aire, triangle, parallélogramme, trapèze, géomtrie dynamique
AIRE DU TRIANGLE
Fichier : Aire triangle 1.fig
Prérequis : Aire du triangle rectangle et distributivité de la multiplication par rapport à l'addition.
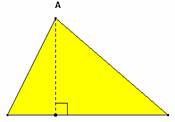
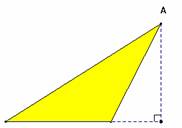
Le point A peut être déplacé. L'aire du rectangle jaune s'obtient soit par l'addition, soit par la soustraction des aires de deux triangles rectangles.Pour établir la formule on utilise alors la distributivité.
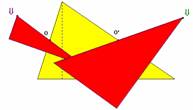
Fichier : Aire triangle 2.fig
Prérequis : Aire du rectangle et symétrie centrale.
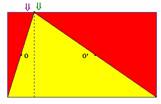
Le déplacement des points indiqués par les flèches permettent de visualiser les symétries de centre O et O'.
La formule est établie à partir de l'aire du rectangle.
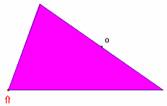
Fichier : Aire triangle 3.fig
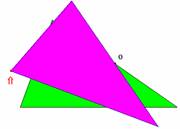
Le déplacement du point indiqué par la flèche permet de visualiser la symétrie de centre O
La formule est établie à partir de l'aire du parallélogramme.
AIRE DU PARALLELOGRAMME
Fichier : Aire parallélogramme 1.fig
Prérequis : Aire du triangle.
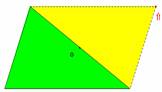
Le déplacement du point indiqué par la flèche permet de visualiser la symétrie de centre O
La formule donnant l'aire du triangle étant connue, en considérant la symétrie de centre O il est possible d'établir la formule de l'aire du parallélogramme.
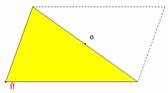
Fichier : Aire parallélogramme 2.fig
Prérequis : Aire du rectangle.
Le déplacement du point indiqué par la flèche permet de visualiser le découpage.
Ne disposant pas de la translation le découpage ne permet pas d'établir la formule de l'aire du parallélogramme, mais permet de la retenir.
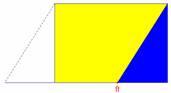
Fichier : Aire parallélogramme 2bis.fig
Prérequis : Aire du rectangle.
Ce fichier est une variante du précédent (autre découpage).
Le point indiqué par la flèche permet de visualiser le découpage.
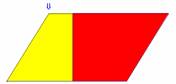
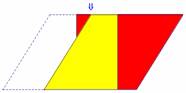
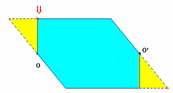
Fichier : Aire parallélogramme 3.fig
Prérequis : Aire du rectangle et symétrie centrale
Le déplacement du point indiqué par la flèche permet de visualiser les symétries.
En utilisant les propriétés de la symétrie centrale la formule de l'aire du parallélogramme peut, par cette méthode, être justifiée.
AIRE DU TRAPÈZE
Fichier : Aire trapèze 1.fig
Prérequis : Aire du triangle
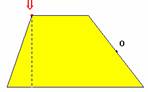
Les points A et B peuvent être déplacés. L'aire du trapèze s'obtient par l'addition des aires des deux triangles.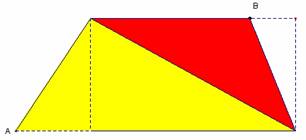
Fichier : Aire trapèze 2.fig
Prérequis : Aire du triangle, aire du parallélogramme.
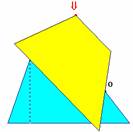
Les points A et B peuvent être déplacés.L'aire du trapèze s'obtient par l'addition de l' aire du parallélogramme à celle du triangle.
Fichier : Aire trapèze 3.fig
Prérequis : Aire du triangle, aire du parallélogramme.
Les points B et C peuvent être déplacés.L'aire du trapèze s'obtient en soustrayant l'aire du triangle à celle du parallélogramme.
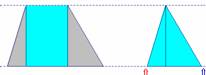
Fichier : Aire trapèze 4.fig
Prérequis : Aire du triangle, aire du rectangle.
Le déplacement des points indiqués par les flèches peuvent être déplacés. Déplacer la flèche bleue le plus possible vers la droite, puis faire de même avec la flèche rouge.L'aire du trapèze s'obtient en ajoutant l'aire du triangle à celle du rectangle.
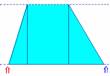
Fichier : Aire trapèze 5.fig
Prérequis : Aire du parallélogramme, symétrie centrale
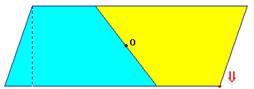
Le déplacement du point indiqué par la flèche permet de visualiser la symétrie de centre O.L'aire du trapèze s'obtient à partir de l'aire du parallélogramme.
Remarque concernant la formule de l'aire du trapèze.
La formule de l'aire du trapèze n'est pas une des compétences exigibles en collège.
Les exemples précédents permettent de l'établir connaissant la grande base, la petite base et la hauteur.
L'exemple 4 proposant un simple découpage, ne permet pas, en toute rigueur, d'établir la formule (on obtient la même expression qu'à l'exemple 2)
Exemple 1 :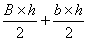 
Exemple 2 :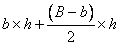 
Exemple 3 :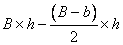 
Exemple 5 : 
G. Bouron
information(s) pédagogique(s)
niveau : 5ème
type pédagogique : non précisé
public visé : non précisé, non précisé
contexte d'usage : non précisé
référence aux programmes :
fichier joint
taille : 121 Ko ;
mathématiques - Rectorat de l'Académie de Nantes