espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > actions nationales 2017-2018
Approximation de e
mis à jour le 29/05/2018
mots clés : approximation, exponentielle, python pour classe,
Objectif
Le but de ce document est de proposer une technique de calcul d’une valeur approchée de e. L’idée est d’effectuer une construction sur papier avant de basculer sous Python pour augmenter le nombre d’étapes de calculs
Activité 1
On se propose de déterminer une approximation du nombre e, image de 1 par la fonction exponentielle. 1.
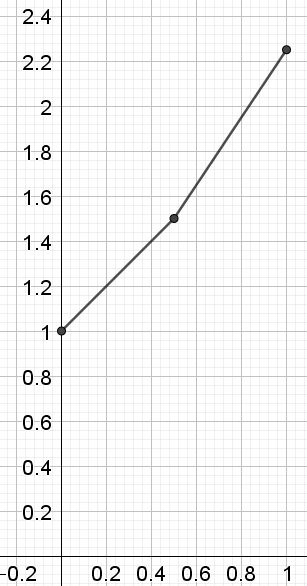
- On partage l’intervalle [0;1] en deux intervalles de même longueur.
- Construire le point A0 d’abscisse 0 de la courbe représentative de la fonction exponentielle.
- Quel est le coefficient directeur de la tangente en A0 ? Tracer cette tangente sur [0; 0,5].
- Placer le point A1 de cette tangente d’abscisse 0,5. Vérifier que l’ordonnée de ce point est 1,5.
- Par définition d’une tangente, ce point A1 est proche de la courbe.
Pour déterminer une approximation de e, on suppose que ce point A1 est un point de la courbe. Expliquer alors pourquoi le coefficient directeur de la tangente en ce point est égal à 1,5. Tracer cette tangente sur [0,5; 1]. - Placer le point A2 d’abscisse 1 de cette tangente. Démontrer que l’ordonnée de ce point est 2,25.
On peut considérer que ce point A2 est proche du point d’abscisse 1 de la courbe. L’ordonnée de ce point est une première approximation pour le nombre e.
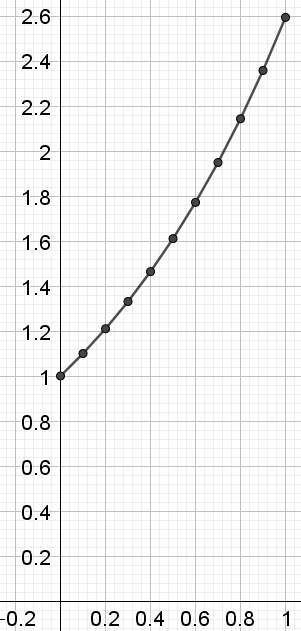
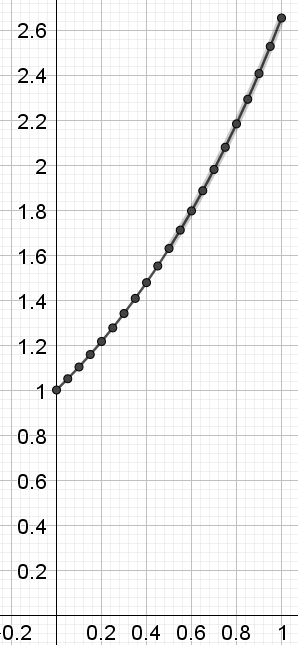
- On partage l’intervalle [0; 1] en n intervalles de même longueur. On reproduit le procédé précédent en approchant la courbe en chaque point Ak(xk; yk) par la tangente en Ak pour k variant de 0 à n -1.
|  |
| Constructions sous GeoGebra | |||
 |  |  |  |
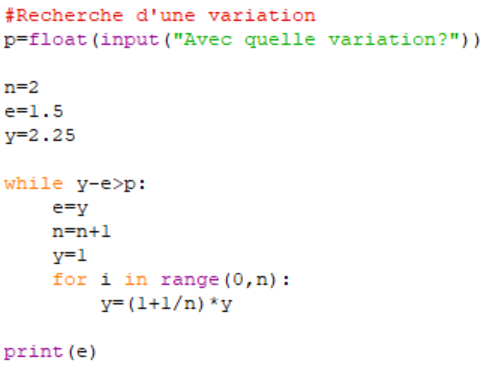
Activité 2
- Modifier le programme précédent pour obtenir une valeur de e avec une précision choisie.
- Modifier la technique précédente pour calculer une valeur approchée de
.
 |  |  |
Hervé DIet, enseignant au lycée Touchard du Mans (72)
information(s) pédagogique(s)
niveau : tous niveaux, Lycée tous niveaux, Terminale, Terminale S, Terminale ES
type pédagogique :
public visé : non précisé, enseignant, élève
contexte d'usage :
référence aux programmes :
page précédente | haut de page
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


