espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2022-2023
étude d'une population
mis à jour le 13/06/2023
mots clés : tableur, big data, tâche complexe

Testée dans 2 classes de 4e au collège Pierre Dubois.
Le but de l'activité est de mettre en évidence qu'avec une série de données on peut dire une chose et son contraire ; il suffit de les exploiter différemment. Il s'agit aussi de réfléchir sur le choix de la modélisation et de comprendre que le choix des données a de l'importance pour faire des prédictions statistiques.
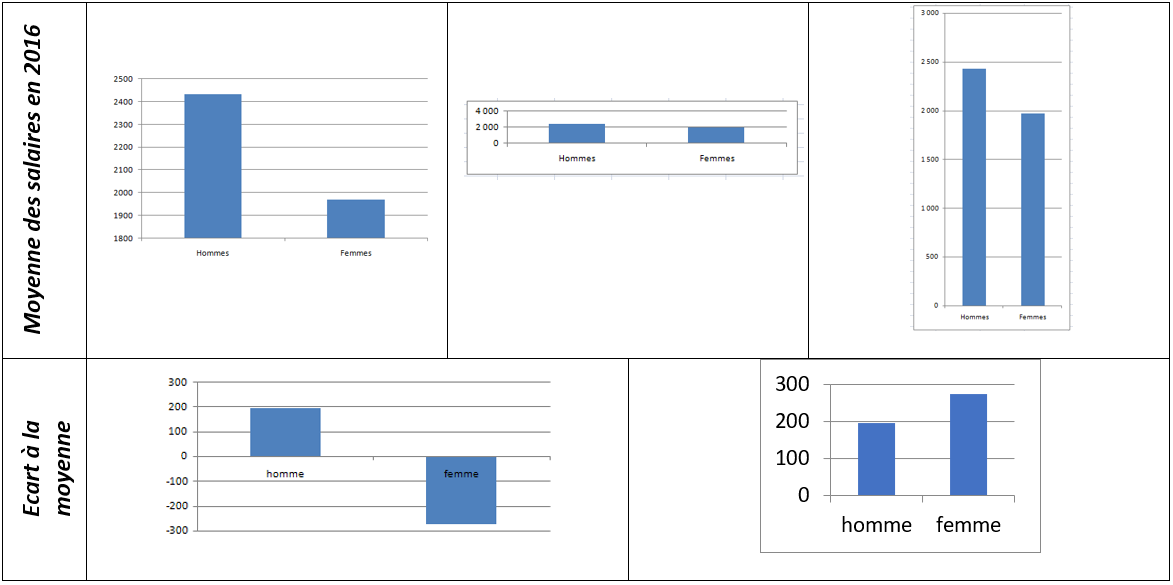
Un travail sur une autre activité (différence de salaire hommes-femmes) a déjà permis de mettre en évidence que le choix de tel ou tel graphique, ainsi que le choix des graduations peut permettre de « fausser » l'impression du lecteur.
2 journalistes veulent chacun écrire un article sur l'évolution de la population mayennaise.
Voici le titre des articles auquel ils ont pensé :
Mme TOUVHABIEN journaliste au journal « L'optimisme Mayennais » a choisi le titre :
Mme SAIPABON journaliste au journal « La morosité de L'ouest » a choisi le titre :
A toi de trouver les arguments !
A l'aide des chiffres qui te sont fournis, tu dois pour chacun des 2 points de vue :
- Faire un graphique représentant l'évolution de la population mayennaise.
- Répondre à la question poser dans le titre de l'article « mais combien sera-t-on en 2030 ? »
Les calculs, les méthodes devront être expliqués clairement sur la copie.
La classe a été répartie en 2 groupes : un qui devait mettre en évidence la croissance de la population mayennaise et un qui devait montrer que la population déclinait. Les groupes ont été faits après un premier temps de recherche individuelle, pendant lequel des élèves ont commencé à exploiter les données brutes et d’autres les écarts entre chaque année. En fonction de la démarche choisie par l’élève je l’ai mis dans le groupe qui correspondait.
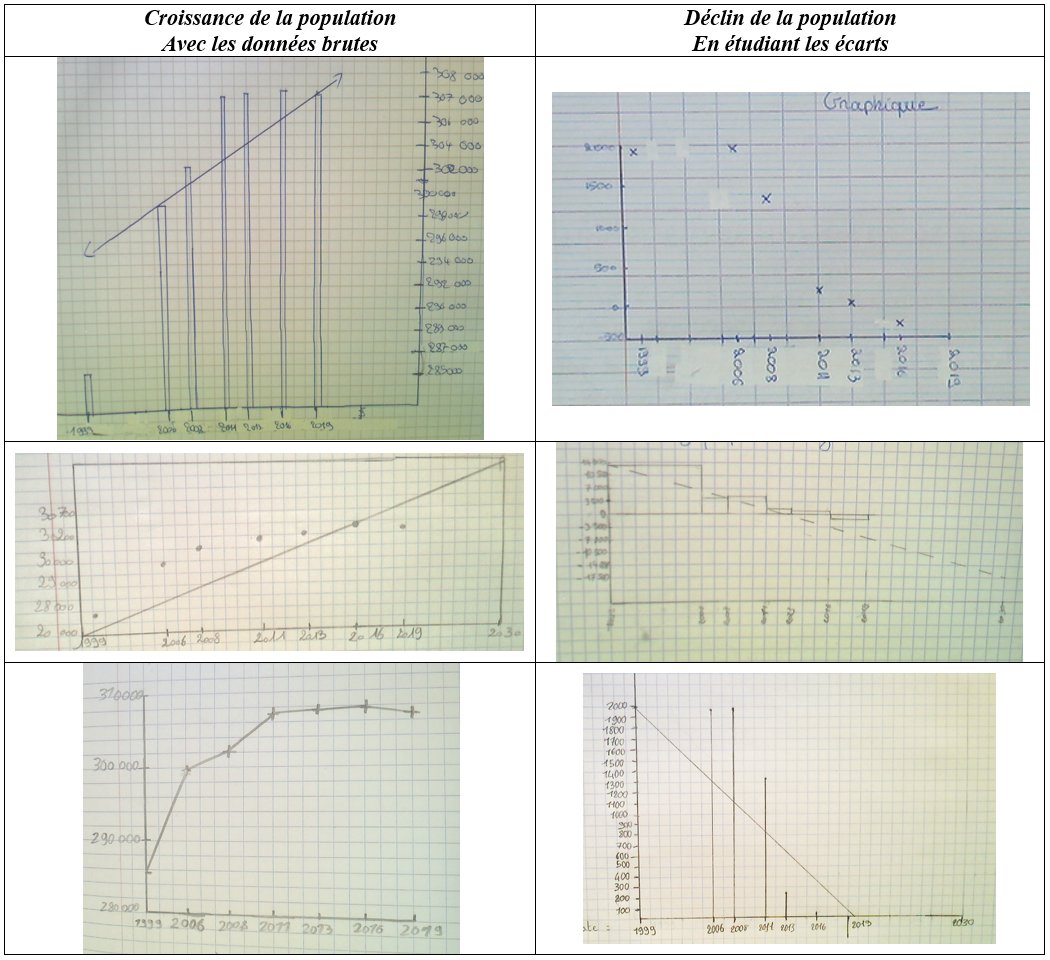
Voici des graphiques réalisés par certains groupes (certains ne sont pas corrects, mais l’idée est intéressante). Un point a été fait en classe pour expliquer le principe de l’ajustement linéaire.
Pour certains élèves qui étudiaient l’écart entre chaque année, il a fallu que je vienne leur expliquer qu’il était plus intéressant de calculer l’écart pour 1 an pour faciliter l’analyse :
| Croissance de la population Avec les données brutes |
| 2 méthodes ont été utilisées par les élèves : certains ont utilisé leur graphique, d’autres ont fait des calculs. |
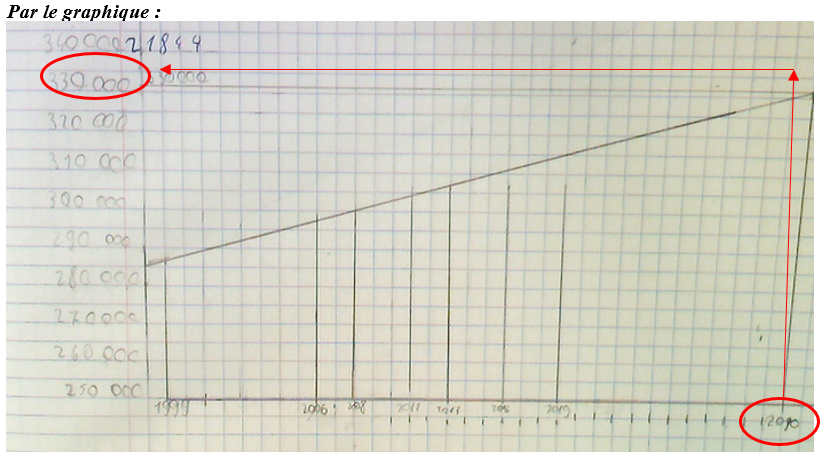 |
 |
| Déclin de la population En étudiant les écarts |
| Les élèves ont tous utilisé le graphique, la difficulté était de comprendre les chiffres qu’ils lisaient sur le graphique, ils ont souvent oublié ou sûrement pas intégré que les baisses qu’on lisait sur le graphique par rapport à l’année d’avant. Ils n’ont pas réussi à trouver et nous avons fait le bilan en plénière. |
| Croissance de la population Avec les données brutes |
| Des élèves ont expliqué les résultats qu’ils ont obtenus sur la croissance de la population mayennaise, en présentant les graphiques, les calculs… Une réflexion sur les écarts trouvés sur le graphique a permis de mettre évidence que la droite choisie n’était pas précise et que cela expliquait les différents résultats. J’ai précisé que dans plusieurs années, ils apprendront une méthode pour avoir une droite « plus » précise. |
| Déclin de la population En étudiant les écarts |
Des élèves ont présenté leurs graphiques en mettant en évidence ce qui leur avait posé problème dans l’activité proposée. Puis une réflexion collective a permis de comprendre bien le graphique et ce que signifiaient les chiffres lus. Nous sommes arrivés à dire « Si entre 2018 et 2019 la population a baissé de 250, entre 2019 et 2020 elle diminuera de 250+250 c'est-à-dire 500 puis entre 2020-2021 elle baissera de 500+250 et ainsi de suite ». Les élèves ont donc pu faire les calculs :  |
Nous avons essayé de répondre à la question : « mais alors, comment savoir le nombre d’habitants qu’il y aura en Mayenne en 2030 et pourquoi on ne réussit pas à trouver ? »
Plusieurs explications ont été données soit par les élèves soit par moi :
- La première idée des élèves a été tout sauf mathématiques « oui, mais avec le Covid il y a eu plus de morts… » ; des explications de la vie courante. Bien que pas mathématiques elles ont forcément une influence et j’ai pu insister sur le fait que c’était une prédiction et on ne pouvait en aucun cas être sûr.
- Une autre explication donnée a été qu’utiliser uniquement les chiffres de la population n’est sûrement pas suffisant, il aurait fallu tenir compte d’autres paramètres.
- Des élèves ont fait remarquer que les données fournies ne formaient pas vraiment une droite, j’ai alors précisé qu’il y avait d’autres manières d’ajuster notamment avec des courbes (sans pour autant rentrer dans les détails).
J’ai alors abordé l’Intelligence Artificielle en leur expliquant que pour qu’elle fonctionne il fallait choisir le meilleur modèle (celui qui s’ajuste le mieux à la réalité) en tenant compte de nombreux paramètres et avec un très grand nombre de données.
J’ai demandé aux élèves de trouver la population en Mayenne en 2050 si on gardait le modèle que l’on avait choisi pour calculer le déclin de la population. Réaction immédiate des élèves : « çà va être long Monsieur !!! ». J’ai alors fait un point sur la méthode qu’avait utilisé Gauss pour calculer 1+2+3+…+99+100 et je leur ai demandé d’appliquer la même méthode pour faire 500+750+1000+…+ 7750+8000, qui correspond à la diminution totale du nombre d’habitants entre 2019 et 2050.
Damien Rivière, enseignant au collège Pierre Dubois - Laval (53)
information(s) pédagogique(s)
niveau : tous niveaux, Cycle 4, 4ème
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA