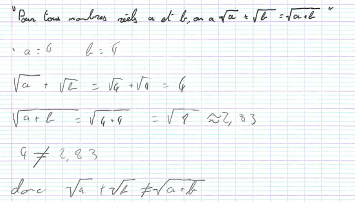espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2023-2024
autour de la notion de preuve ou de l'art de convaincre en mathématiques
mis à jour le 21/05/2024
Exemples de situations à faire vivre au lycée pour développer la notion de preuve, l’intérêt de la démonstration et l’esprit critique des élèves.
mots clés : TraAM, esprit critique, démonstration, conjecture, questions rapides

Expérimentation testée en classe de 2nde GT
- Temps 1 : Des exemples de questions « rapides » étudiées par les élèves
- Temps 2 : Des exemples de situation qui peuvent laisser à penser que tout est vrai (car un grand nombre de situations sont vraies) mais pour lesquelles un contre-exemple (un peu dur à trouver) prouve que ça ne va pas…
- Temps 3 : De l’intérêt de la démonstration
- Temps 4 : De la notion de conjecture ou quand les mathématiques vivent (et que l’on n’a pas encore prouvé…)
1) Exemples de situation à faire vivre en classe
(recherche / décision / argumentation / rédaction / interaction / prise de parole orale)
Situation / mise en oeuvre
- Chaque élève tire au sort une des 7 affirmations ci-dessous et a pour mission de trouver si elle est vraie ou fausse.
- Les élèves doivent s’emparer de l’affirmation, réfléchir à une réponse et préparer/rédiger une argumentation pour convaincre un autre élève (qui travaille sur une autre affirmation).
- Un temps d’échange oral par binôme d’élève est organisé (chaque élève présente l’affirmation qu’il a eu à étudier et essaye de convaincre son interlocuteur de sa réponse « vrai » ou « faux »)
Liste des affirmations proposées
« La somme de trois entiers consécutifs est un multiple de 3 »
« Les nombres premiers sont tous impairs »
« Les nombres entiers ont tous un nombre pair de diviseurs »
« Pour tous nombres réels positifs ou nuls a et b, on a »
« Le carré d’un nombre impair est un nombre impair »
« Pour tous nombres réels a et b, on a : »
« Pour tous nombres réels a, b et c, on a : »
Exemples de production d’élèves
Voici quelques traces des travaux d’élèves (qui avaient pour mission de préparer un échange oral avec leur camarade) :
Conclusion et bénéfices didactiques du temps 1
La notion de contre-exemple semble convaincre les élèves et apparait comme opérante pour convaincre qu’une propriété est fausse. Ainsi, lors de la mise en commun qui fait suite aux échanges entre élèves, il apparait que les propriétés :
« Les nombres premiers sont tous impairs »
« Les nombres entiers ont tous un nombre pair de diviseurs »
« Pour tous nombres réels positifs ou nuls a et b, on a »
« Pour tous nombres réels a, b et c, on a : »
sont fausses car les élèves ont facilement trouvé un cas qui contredit l’affirmation.
Pour les propriétés envisagées comme « vraie » (les trois autres), les arguments sont, à cet instant, variés :
- Multiplicité d’exemples : le carré de 7 c’est 49 c’est impair, le carré de 13 c’est 169 c’est impair…
- Tentative de disjonction des cas (« le carré d’un nombre finissant par un 1 finit par un 1, le carré d’un nombre finissant par un 3 finit par un 9…)
- Argument type « c’est une propriété du cours donc c’est vrai… ». « On l’a écrit dans le cours et le prof de maths l’a dit donc c’est vrai… »
2) Des situations « piège »
(recherche / décision / argumentation / rédaction / interaction / prise de parole orale)
Situation / mise en œuvre :
On réitère le procédé en faisant tirer aux élèves une situation parmi les 4 suivantes, avec la même consigne : l’affirmation est-elle vraie ou fausse ? Trouver des arguments pour convaincre votre entourage.
Note : Ces situations paraissent vraies (les premiers essais des élèves peuvent laisser à croire ceci) mais elles sont fausses pour des cas « peu facile à trouver »….
Liste des affirmations proposées
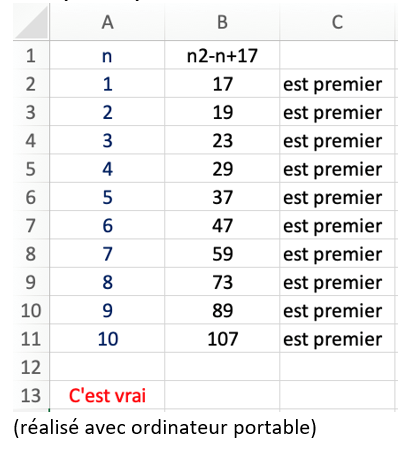
- « Si n est un entier alors
est un nombre premier »
- « Les nombres de Fermat
avec n un entier sont des nombres premiers »
- « Les nombres de Mersenne
avec n premier sont des nombres premiers »
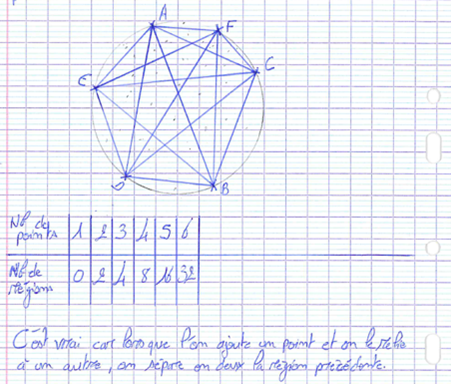
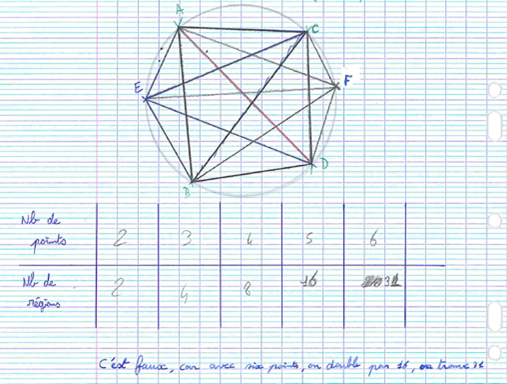
- « Quand on cherche combien il y a de régions d’un disque déterminées par toutes les cordes joignant des points deux à deux, on remarque qu’on double le nombre de régions quand on rajoute un point »
Exemples de production d’élèves
Conclusion et bénéfices didactiques
La plupart des élèves n’ont pas trouvé de contre-exemple aux affirmations proposées.
La 4ème situation a donné lieu à un phénomène intéressant : une partie des élèves avaient trouvé 31 régions pour 6 points, d’autres 32 régions car ils « avaient envie » de trouver 32 ou se disaient que 31 étaient une erreur de dénombrement de leur part.
Montrer aux élèves que les contre-exemples étaient difficile à trouver (certains élèves avaient été persévérant ou bien inspirés…) a permis de développer leur esprit critique, leur prudence avec d’affirmer qu’une propriété est vraie.
L’importance d’une démonstration est alors apparue.
La notion de conjecture comme propriété qui semble vraie mais qu’on ne parvient pas à démontrer a été évoquée.
Éléments de correction : Nombre de Mersenne M11 non premier
3) Les démonstrations au programme du lycée
En 2nde :
- Le nombre 1/3 n’est pas décimal.
- Le nombre racine de 2 est irrationnel.
- Quel que soit le réel a, la somme de deux multiples entiers de a est un multiple de a.
- Le carré d’un entier impair est un entier impair.
- Quels que soient les réels positifs a et b, on a :
- Pour tous réels a et b strictement positifs, on a :
- Illustration géométrique de l’identité remarquable (a+b)2 = a2 + 2ab + b2 lorsque a et b sont positifs.
- Deux vecteurs (du plan) sont colinéaires si et seulement si leur déterminant est nul.
- Le projeté orthogonal d’un point M sur une droite
est le point de la droite
le plus proche du point M.
- Relation trigonométrique pythagoricienne
dans un triangle rectangle.
- En utilisant le déterminant, établir la forme générale d’une équation de droite, dans le plan.
- Étudier la position relative des courbes d’équation y = x ; y = x2 ; y = x3 pour x positif.
- Sens de variation des fonctions carré, inverse et racine carrée.
4) De la notion de conjecture : Goldbach, Syracuse et leurs amis…
Prolongement : montrer aux élèves des situations qui semblent vraies ou des problèmes dont on connait la réponse mais que les mathématiques n’ont pas encore démontrées (notion de conjecture…)
Dire que les mathématiques sont vivantes…
La conjecture de Goldbach
« Tout entier pair supérieur ou égal à 4 peut s'écrire comme la somme de deux nombres premiers. »
La conjecture de Syracuse
Une suite de nombres est définie de la façon suivante :
- on choisit un entier strictement positif u0
- si u0 est pair, on pose u1 = u0/2. Sinon, on pose u1 = 3u0 + 1
- si u1 est pair, on pose u2 = u1/2. Sinon, on pose u2 = 3u1 + 1
- on procède de la même façon pour construire un+1 à partir de un
La conjecture de Syracuse consiste à affirmer que pour n'importe quelle valeur de u0, la suite correspondante prendra la valeur 1 à un certain moment.
La conjecture de Fermat (démontrée en 1994)
La conjecture de Fermat, consistait à dire que quel que soit l'exposant entier n > 2, il est impossible de trouver des entiers non nuls a, b, c tels que an + bn = cn.
La quadrature du cercle (démontrée en 1882)
Le problème de la quadrature du cercle est un très vieux défi géométrique : il consiste, étant donné un disque, à essayer de construire, à l'aide d'un compas et d'une règle (non graduée) seulement, un carré dont l'aire est égale à celle du disque donné.
Stéphane Percot, enseignant au lycée Rosa Parks - La Roche-sur-Yon (85)
information(s) pédagogique(s)
niveau : tous niveaux, 2nde
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA