 | 
BTS SN – Interprétation de la lecture graphique d'un signal
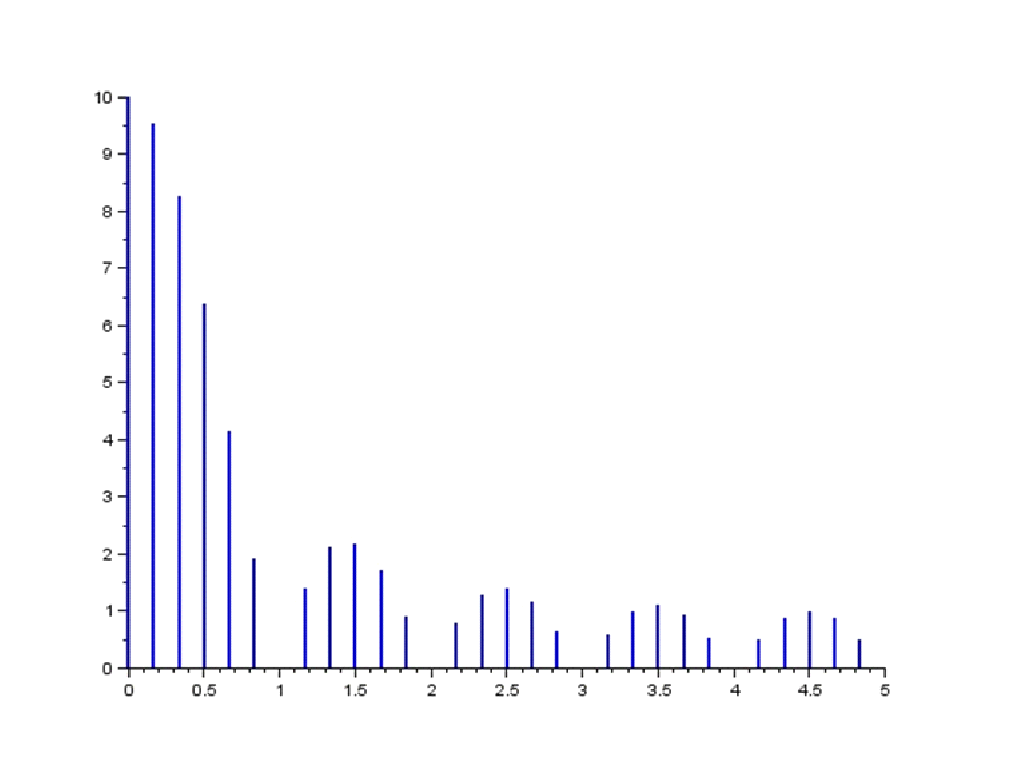
Le but de cette activité est d'observer les particularités graphiques de la TFD d'un signal et d'en justifier certaines via un calcul.
Situation d'accroche : le graphique ci-dessus représente la transformée de Fourier discrète d'un signal. Il s'agit d'observer les particularités de ce graphique et de conduire des calculs permettant de les justifier mathématiquement. |
 |
BTS SN – Transformée de Fourier discrète et analyseur de spectre
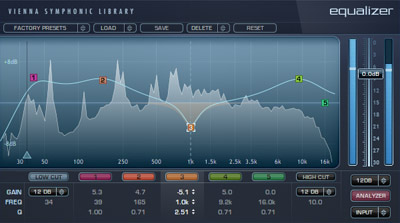 Le graphique ci-contre représente la TFD d’un signal audio donné par un logiciel. On y fait un traitement numérique audio d’égalisation (courbe numérotée 1-2-3-4-5) qui consiste à amplifier ou atténuer avec précision certaines fréquences contenues dans le signal audio (enveloppe en arrière plan donnée par une TFD). Le graphique ci-contre représente la TFD d’un signal audio donné par un logiciel. On y fait un traitement numérique audio d’égalisation (courbe numérotée 1-2-3-4-5) qui consiste à amplifier ou atténuer avec précision certaines fréquences contenues dans le signal audio (enveloppe en arrière plan donnée par une TFD).
Cette représentation du spectre d’amplitude est utilisée par les analyseurs de spectre qui réalise une TFD (c’est le cas pour les appareils utilisés en physique. Connaître les propriétés de la TFD permet de mieux interpréter des choix de paramétrage des appareils, choix associés à l’interprétation de la visualisation obtenue par TFD).
|
 |
Décomposition de Fourier discrète
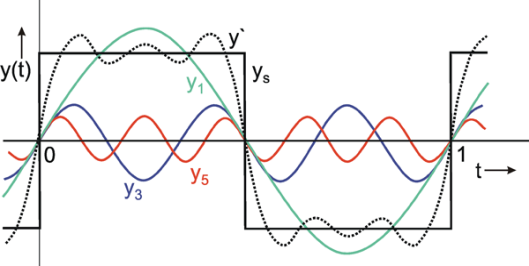 Le graphique ci-contre représente les trois premiers termes sinusoïdaux de la décomposition de Fourier dans le domaine analogique d’un signal carré ainsi que la somme de ces trois termes. On peut trouver dans l’exploitation de la TFD une équivalence dans le domaine numérique. Le graphique ci-contre représente les trois premiers termes sinusoïdaux de la décomposition de Fourier dans le domaine analogique d’un signal carré ainsi que la somme de ces trois termes. On peut trouver dans l’exploitation de la TFD une équivalence dans le domaine numérique.
Les représentations fréquentielles en amplitude et en phase, d’un signal analogique périodique, utilisées en physique permettent d’obtenir la décomposition de Fourier (composante continue, fondamental et harmoniques).
On peut utiliser le module et la phase de la TFD pour trouver dans le domaine numérique une décomposition de Fourier équivalente à celle utilisée dans le domaine analogique, son échantillonnage reconstituant le signal numérique.
|
 | 
Transmission des données numériques
Le but de cette activité est d’ étudier l’influence de la rapidité de transmission d’une donnée numérique se déplaçant sur des réseaux informatiques.
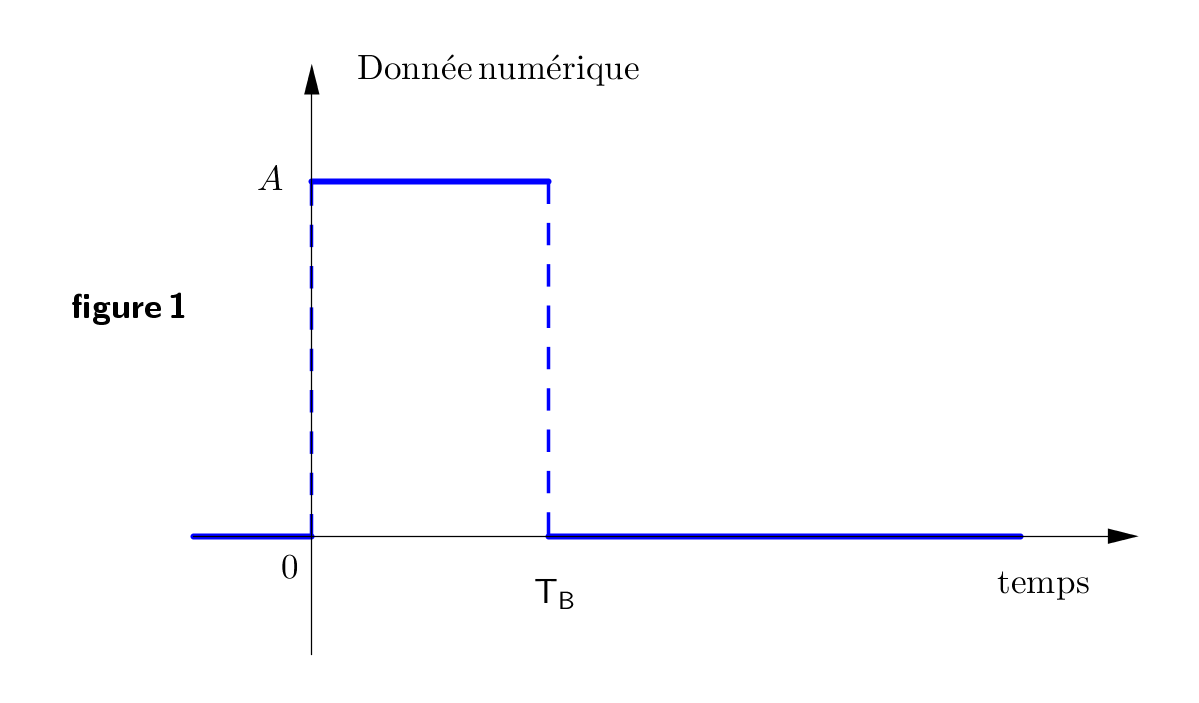
Situation d'accroche : On modélise cette donnée par une simple impulsion carrée (figure ci-contre) représentant le bit 1 transmis.
On prendra 10 x Te = TB où : - TB est la durée d’un bit transmis ; (Fe = 10 x FB, le théorème de Shannon est vérifié : Fe >= Fmax)
- Te est la période d’échantillonnage.
|
 | 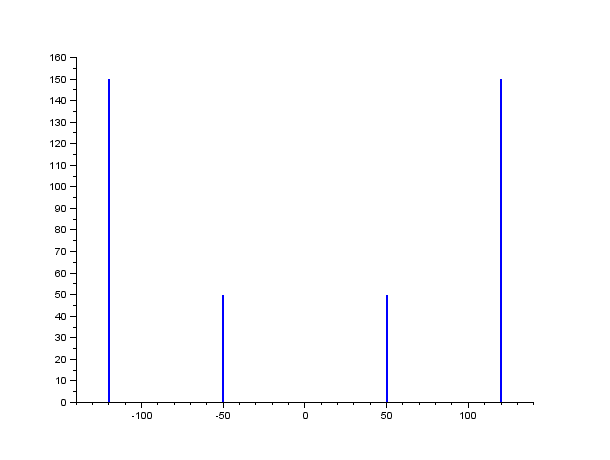
TFD d’un signal périodique
L’objectif de cette fiche est de montrer aux étudiants comment l’on peut utiliser la TFD pour retrouver le spectre d’un signal périodique.
|
 |
TFD algorithmes calculatrices
L’activité propose d’analyser la formule de calcul de la TFD par le biais d’un algorithme. L’étudiant doit élaborer ensuite un autre algorithme pour constituer un échantillon provenant d’un signal continu.
L’activité peut venir compléter des exercices de calcul de la TFD « à la main » et servir d’introduction à l’utilisation de la commande fft des logiciels de calcul numérique ou formel. |
| | 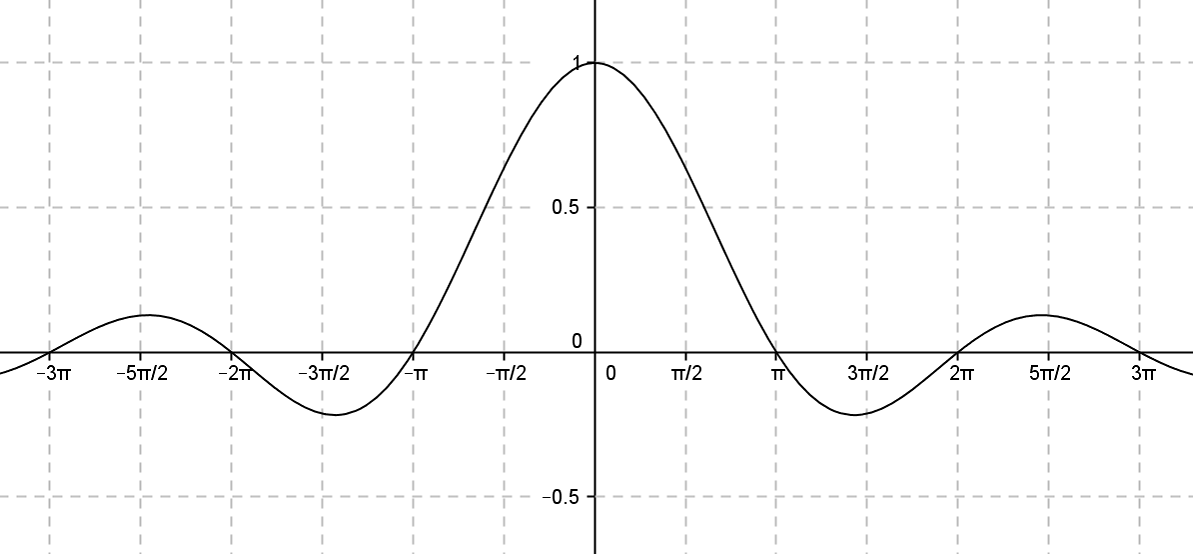 Fonction Sinus Cardinal Fonction Sinus Cardinal La fonction sinus cardinal intervient chaque fois que l’on calcule le spectre d’un signal obtenu par troncature (sur un temps d’acquisition limité). L’objectif, pour cette fiche, est d’étudier quelques propriétés de la fonction sinus cardinal et, en guise d’application, de justifier que la TFD renvoie le spectre de raies d’un signal périodique si celui-ci est observé sur un durée égale à un multiple de sa période (on suppose que la condition de Shannon est réalisée). |
| | 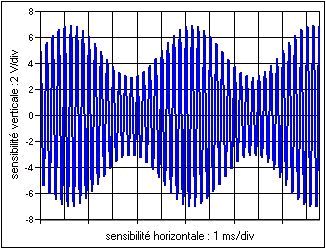 Modulation sans porteuse Modulation sans porteuse L’objectif de cette fiche est d’appliquer la TFD dans le cadre de la modulation d’un signal porteur par un message à transmettre. L’exemple d’étude proposé est très schématique et illustre simplement le principe. La transmission étudiée est une modulation dite « sans porteuse ». |
| | 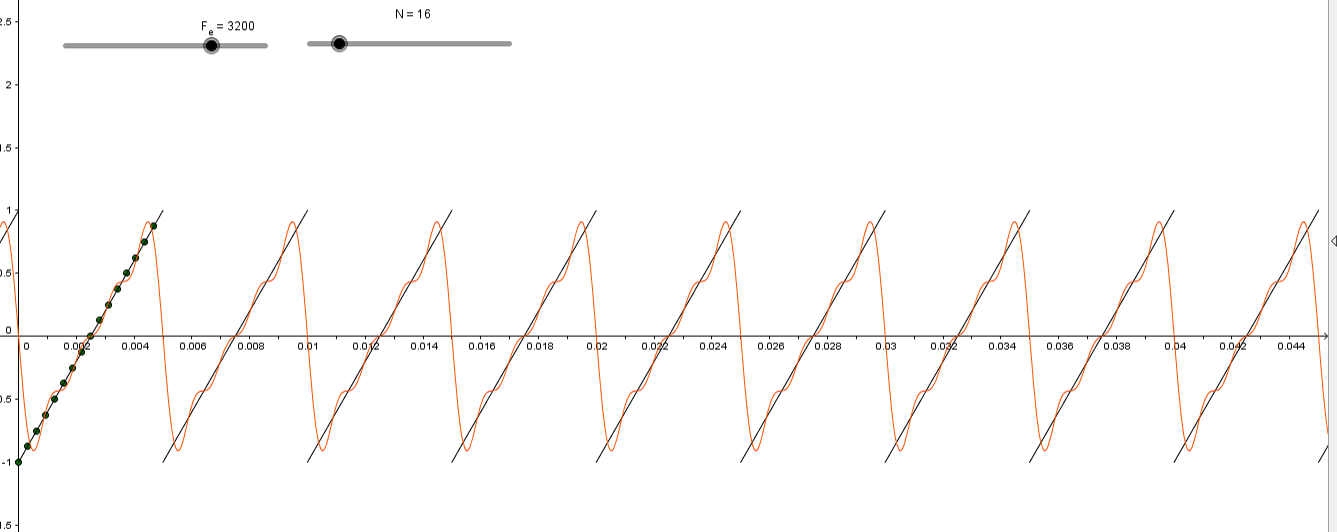
Extraction d'un fondamental Extraire le fondamental d'un signal périodique. Lien avec les coefficients d'une série de Fourier. |
| | 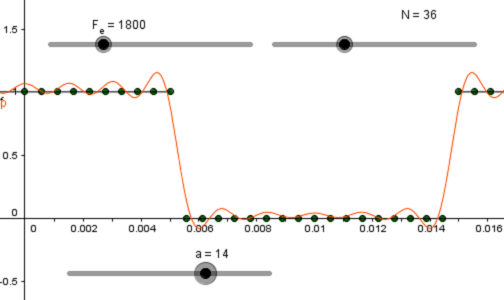 Des séries de Fourier à la TFD Des séries de Fourier à la TFD Le but de cette fiche est d'expliquer, dans un cas particulier, la signification des nombres complexes obtenus par TFD. |
| | 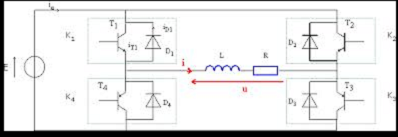 Spectre d'un signal onduleur par une charge RL Spectre d'un signal onduleur par une charge RL Le but de cette activité est l'analyse harmonique d'un signal et de relier les coefficients de Fourier(vu en physique) avec ceux obtenus par TFD. Une question de mathématiques prolongeant cette étude, portant sur la fonction de transfert (nombres complexes)peut être proposée pour poursuivre ce travail. |
| | 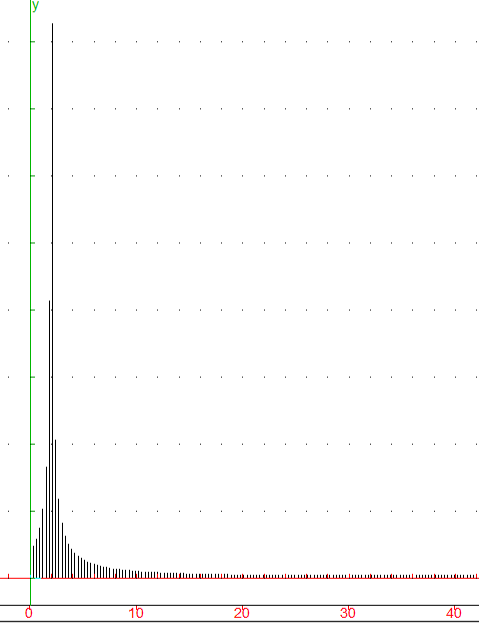 TFD d'une exponentielle complexe TFD d'une exponentielle complexe Le but de cette activité est d'introduire la notion d'impulsion de Dirac par la TFD d'une exponentielle complexe et surtout de comprendre la TFD d'une sinusoïde. |
| | 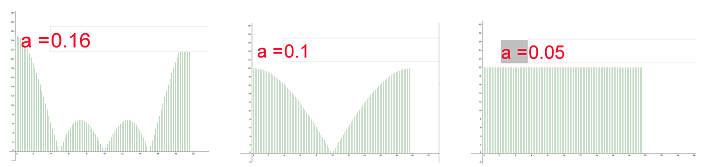 Impulsion de Dirac Signal porte Impulsion de Dirac Signal porte Définir l'impulsion de Dirac vue en physique. |
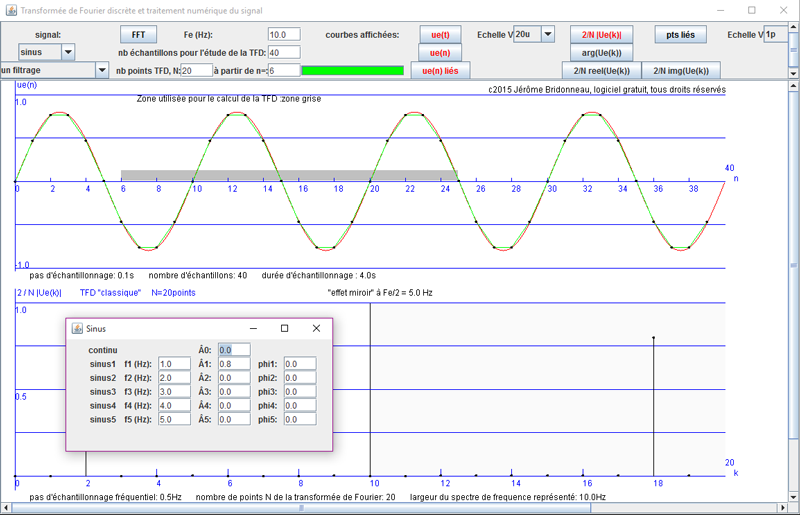
 Ce logiciel (cliquer sur l'image pour le télécharger) fait le lien entre les mathématiques et la physique appliquée pour la transformée de Fourier discrète (programme de mathématique en BTS SN option IR). Il peut aussi servir en physique appliquée pour des parties de cours sur le signal numérique, l'échantillonnage, le traitement numérique et la représentation fréquentielle.
Ce logiciel (cliquer sur l'image pour le télécharger) fait le lien entre les mathématiques et la physique appliquée pour la transformée de Fourier discrète (programme de mathématique en BTS SN option IR). Il peut aussi servir en physique appliquée pour des parties de cours sur le signal numérique, l'échantillonnage, le traitement numérique et la représentation fréquentielle.  Mode d'emploi du logicel TFD
Mode d'emploi du logicel TFD
 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

 Le graphique ci-contre représente la TFD d’un signal audio donné par un logiciel. On y fait un traitement numérique audio d’égalisation (courbe numérotée 1-2-3-4-5) qui consiste à amplifier ou atténuer avec précision certaines fréquences contenues dans le signal audio (enveloppe en arrière plan donnée par une TFD).
Le graphique ci-contre représente la TFD d’un signal audio donné par un logiciel. On y fait un traitement numérique audio d’égalisation (courbe numérotée 1-2-3-4-5) qui consiste à amplifier ou atténuer avec précision certaines fréquences contenues dans le signal audio (enveloppe en arrière plan donnée par une TFD).  Le graphique ci-contre représente les trois premiers termes sinusoïdaux de la décomposition de Fourier dans le domaine analogique d’un signal carré ainsi que la somme de ces trois termes. On peut trouver dans l’exploitation de la TFD une équivalence dans le domaine numérique.
Le graphique ci-contre représente les trois premiers termes sinusoïdaux de la décomposition de Fourier dans le domaine analogique d’un signal carré ainsi que la somme de ces trois termes. On peut trouver dans l’exploitation de la TFD une équivalence dans le domaine numérique.

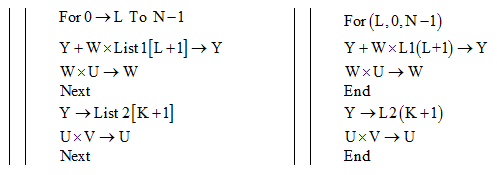
 Fonction Sinus Cardinal
Fonction Sinus Cardinal



 Spectre d'un signal onduleur par une charge RL
Spectre d'un signal onduleur par une charge RL
