- Collèges tous niveaux
- préparation pédagogique
- enseignant
construire des leçons sur le dessin - 10
des lignes, des traces issues de la géométrie.

| "La ligne géométrique est un être invisible. Elle est la trace d'un point en mouvement, donc son produit. Elle est née du mouvement - et cela par l'anéantissement de l'immobilité suprême du point. Ici se produit le bond du statique vers le dynamique." V. Kandinsky Point, ligne, plan |
"Une ligne unit autant qu'elle divise" Brusatin, Histoire de la ligne.
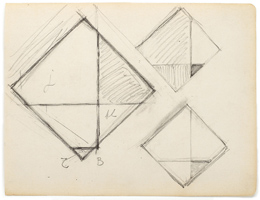 Piet Mondrian Carnet de dessin 1925 |
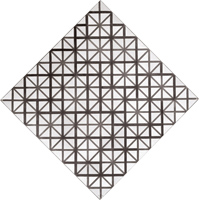 Piet Mondrian Trois compositions dans le losange1926 |
 Sol Lewitt Lines to Points on a GridWall Drawing 1975 |
 monolithes de Gavrinis 3000 ans av.JC |
 Franck Stella Mas o Menos 1964 acrylique sur toile 300x418 cm centre Pompidou Paris |
 Denis Oppenheim Cancelled Crop 1969 |
 Eliezer Lissitzky Prounen raum 1923 reconstitution 1971, bois peint 320x364x364 Tate Gallery, Londres. |
 François Morellet L'Avalanche, 1996 36 tubes d'argon bleu, fils de haute-tension blancs |
 François Morellet |
| Alors qu'aujourd'hui 'tout est permis, François Morellet, a voulu au contraire restreindre de la manière la plus stricte les moyens de l'artiste : il utilise les contraintes d'un système et de la géométrie, afin de parvenir à formuler un art contrôlé", précise Serge Lemoine dans une monographie* qu'il consacre à l'artiste. La ligne est droite ou courbe, horizontale, verticale ou inclinée ; elle ne se trace pas seulement à la craie ou au pinceau, mais peut être formée de bois, de néon ou d'acier. De fait, Morellet s'inscrit très tôt dans la tendance de l'art abstrait géométrique d'un Max Bill ou d'un Piet Mondrian, qu'il découvre dans les années 1950 - il a alors 25 ans. Il tient d'eux la volonté d'élaborer son travail à partir d'une formule mathématique, d'un système plus ou moins farfelu et souvent révélé par les titres mêmes des créations. |
 Felice Varini trois cercles désaxés 2005 |
Géométrie, géométrique , géométrisme
d'après Vocabulaire d'esthétique - Souriau
"Les figures géométriques
Elles présentent des propriétés esthétiques importantes. D'abord ce sont de "bonnes formes" selon l'expression gestaltiste : formes claires, facilement perceptibles,et qui ressortent nettement dans les ensembles.
de plus, elles ont de nombreuses propriétés mathématiques et cela leur permet des usages multiples. En fin, elles sont d'une grande fécondité, c'est à dire qu'elles prêtent à des compositions en dispositions irrégulières."
Elles présentent des propriétés esthétiques importantes. D'abord ce sont de "bonnes formes" selon l'expression gestaltiste : formes claires, facilement perceptibles,et qui ressortent nettement dans les ensembles.
de plus, elles ont de nombreuses propriétés mathématiques et cela leur permet des usages multiples. En fin, elles sont d'une grande fécondité, c'est à dire qu'elles prêtent à des compositions en dispositions irrégulières."
| Comment le dessin géométrique peut-il structurer un espace . |
| Comment le jeu des lignes peut-il unir un espace (Varini, Lissitzki) le diviser (Morellet, Buren), le structurer (Gavrinis, Stella), le révéler (Stella, Varini, Sol Lewitt). |
objectifs
| amener les élèves à considérer le dessin géométrique comme un matériau de création possible. |
| prendre conscience que le dessin de lignes géométriques peut modifier la perception d'un espace. |
| différencier dessin géométrique créant des motifs décoratifs et dessin géométrique constituant d'une œuvre |
programme
| en 3e transformer la perception d'un espace |
| en seconde dans toutes les civilisations, la relation qu'entretient l'homme avec le monde s'illustre par la manière dont il conçoit et représente l'espace. Qu'elle ait une origine cosmogonique, symbolique, poétique, ou qu'elle semble écouler d'une approche rationnelle du réel et des phénomènes optiques, la représentation de l'espace repose nécessairement sur un système qui produit des équivalents plastiques. On observera que le dessin génère également son propre espace, son propre système, qu'il migre d'un support à l'autre, révèle ce support ou parvient à s'en dégager. |
auteurs :
InSitu collège
Mots clés :

