- tous niveaux
- Terminale
- non précisé
Découverte de la convexité en terminale spécialité
Cet espace pédagogique a été conçu pour accompagner votre formation professionnelle, vous proposer des ressources pédagogiques et vous permettre de vous tenir informés des actualités de nos disciplines.
Cette activité permet aux élèves de construire en autonomie le concept de convexité à travers des exemples.

Les objectifs
- Travailler en autonomie
- Réactiver les notions de variations d’une fonction, de fonction dérivée, de tangentes à une courbe
- Construire des représentations du concept de convexité
- Aboutir à une méthode efficace et pérenne pour étudier la convexité d’une fonction Stratégie utilisée pour présenter la situation aux élèves
- Énoncé distribué à chaque élève (voir en pièce jointe)
Éléments de mise en œuvre
- Aucun travail préalable sur cette notion n’a été fait.
- La séance dure environ une heure, en classe entière.
- Les élèves travaillent seuls, en autonomie.
- L’exercice final est à finir ou à traiter à la maison.
- Le travail à la maison demandé est le suivant : rédiger sur une feuille simple sa propre trace de cours sur le thème « CONVEXITÉ D’UNE FONCTION ».
Cette trace est à remettre au professeur pour validation. - Une trace de cours d’un(e) élève est ensuite choisie collectivement pour être mise en ligne et accessible à tous.
Le TP découverte de la convexité en terminale spécialité
I – Vocabulaire
Observer les 5 graphiques ci-dessous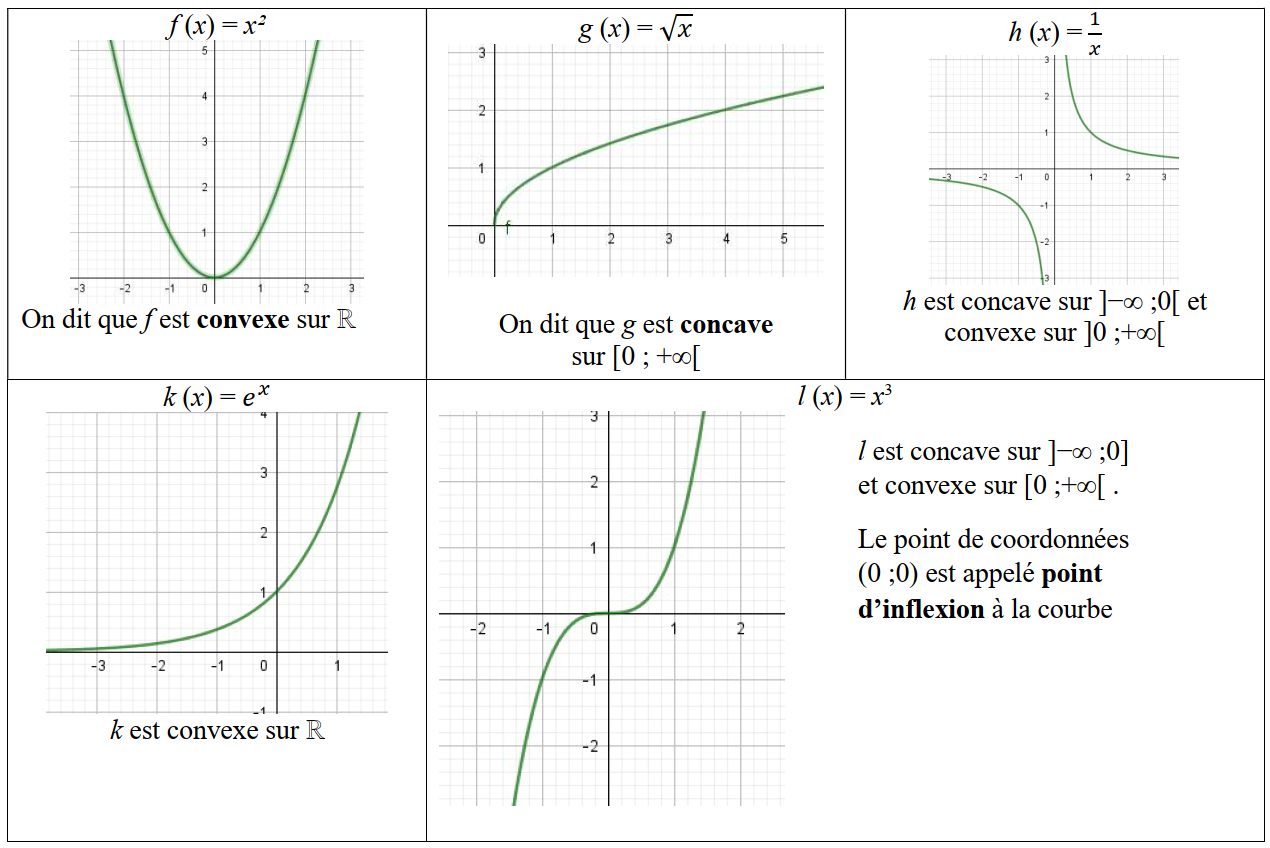
A faire vous-même 1
Pour les 3 courbes suivantes, dire si elles sont convexes ou concaves et préciser sur quels intervalles.Possèdent-elles des points d’inflexion ? Lesquels ?
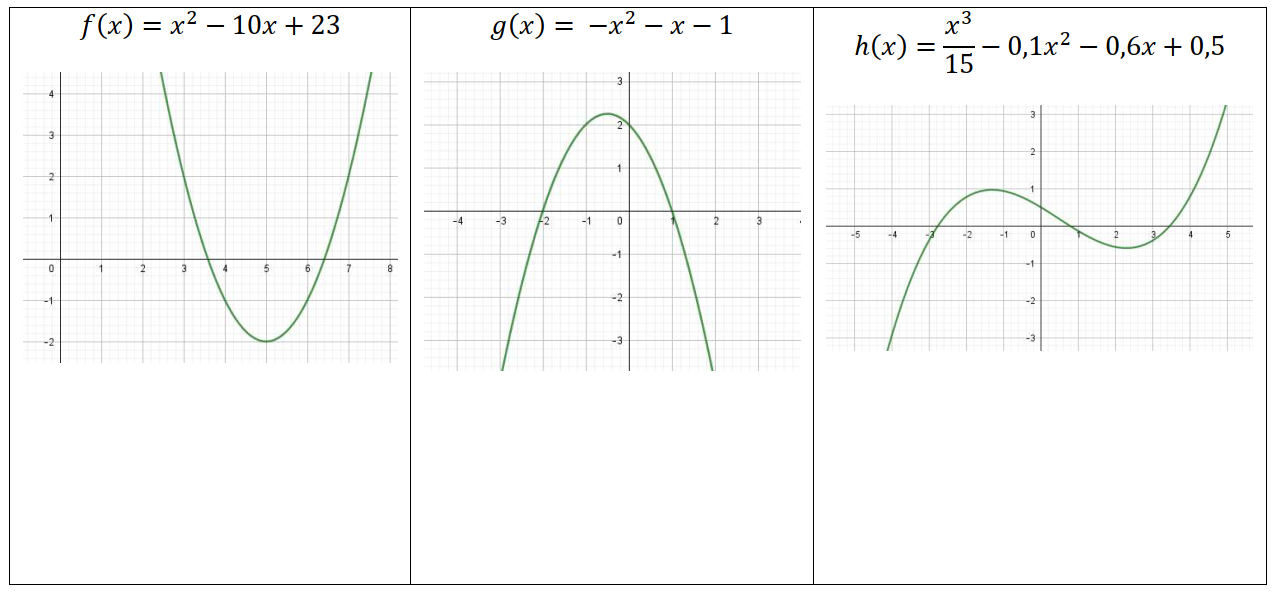
II – Vitesse de croissance
A faire vous-même 2
Reprenons plus en détail la fonction carrée et la fonction racine carrée.Pour chacune d’entre elle, compléter les tableaux ci-dessous qui mettront en évidence les écarts entre les images de deux nombres x espacés de 1 unité ( f (1) - f (0) ; f (2) - f (1) ; etc)
Compléter alors les phrases inscrites sous les courbes.
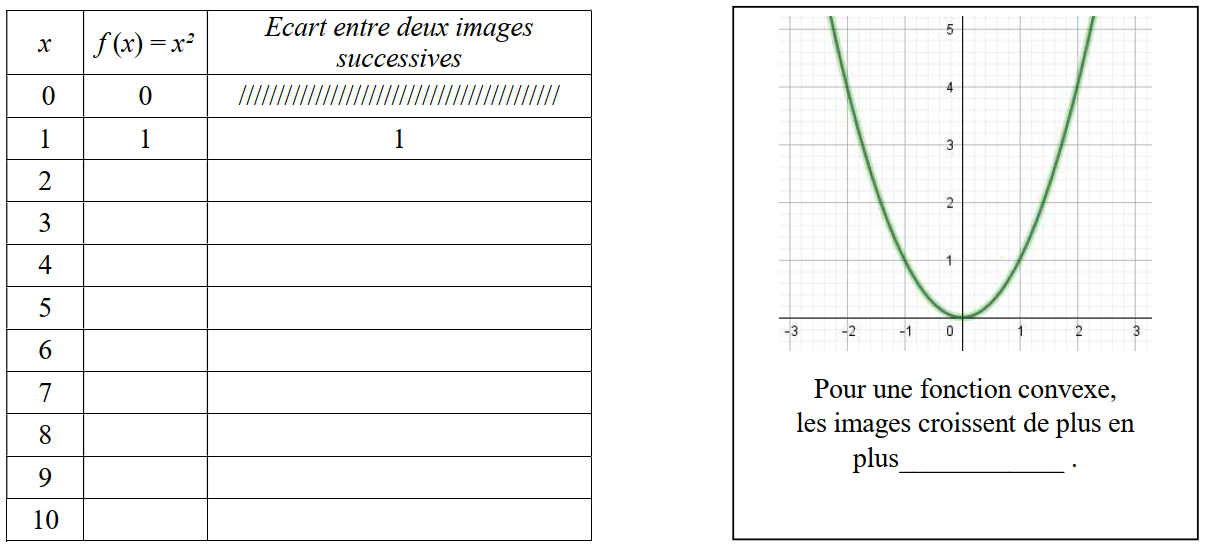
Pour le tableau ci-dessou, donner des valeurs approchées au besoin.
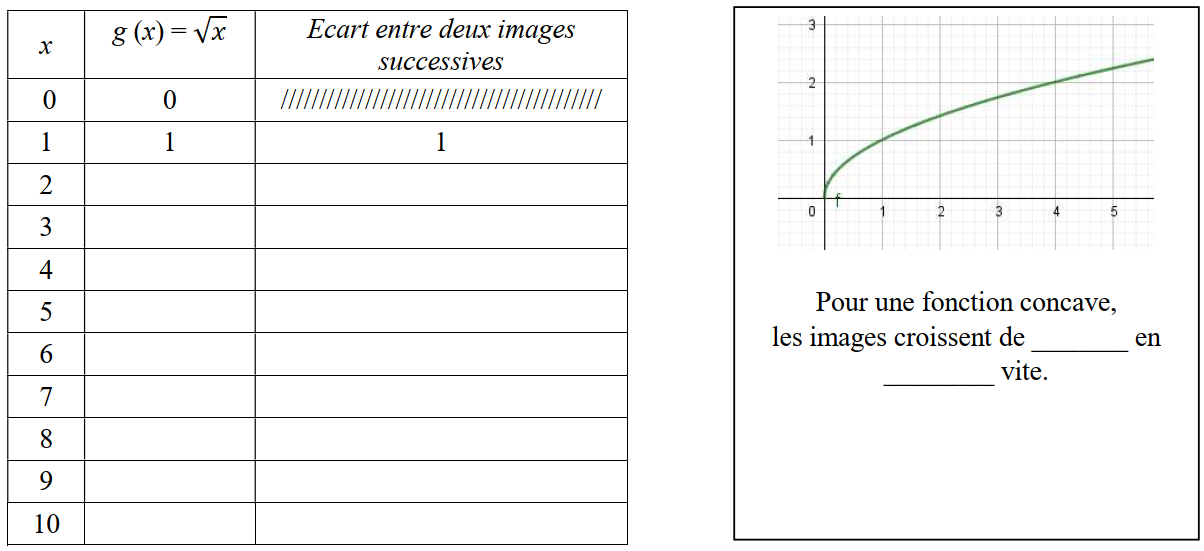
III – Lien entre convexité et dérivation
Toujours pour la fonction carrée f (x) = x² et la fonction racine carrée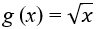
A faire vous-même 3
Compléter le tableau suivant
Sur le graphique ci-dessous, tracer alors les 5 tangentes aux points d’abscisses -3 ; -1 ; 0 ; 1 et 2
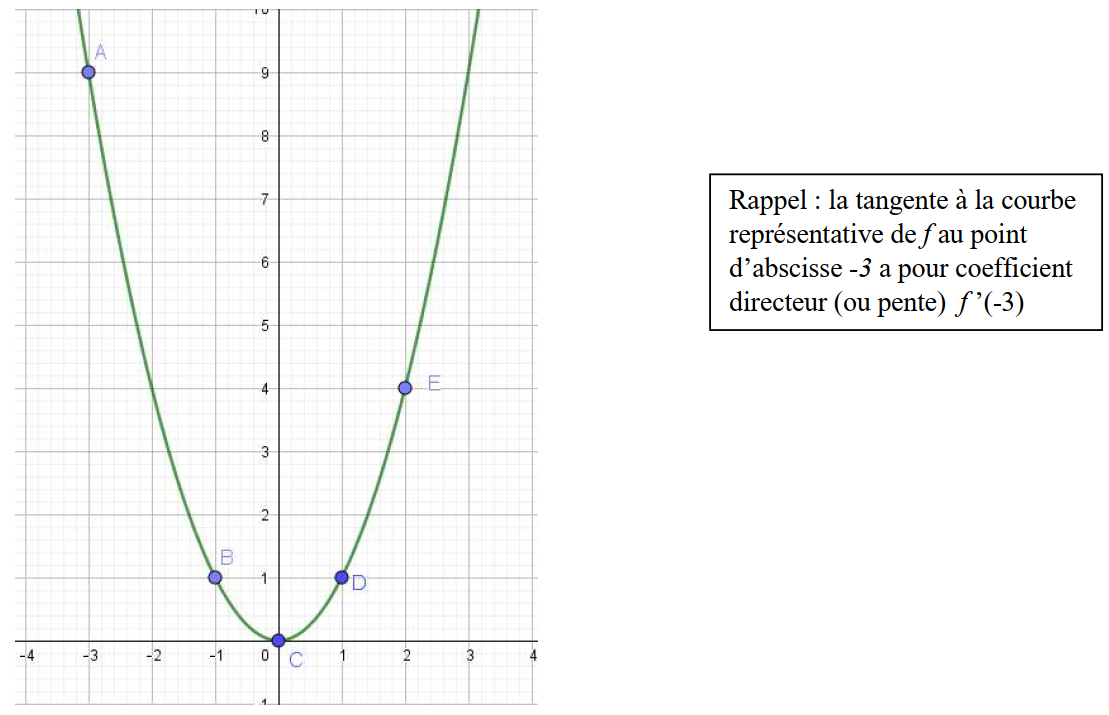
A faire vous-même 4
Compléter le tableau suivant
Voici la représentation graphique de g et de ses tangentes aux points d’abscisses 0,5 ; 4 et 9
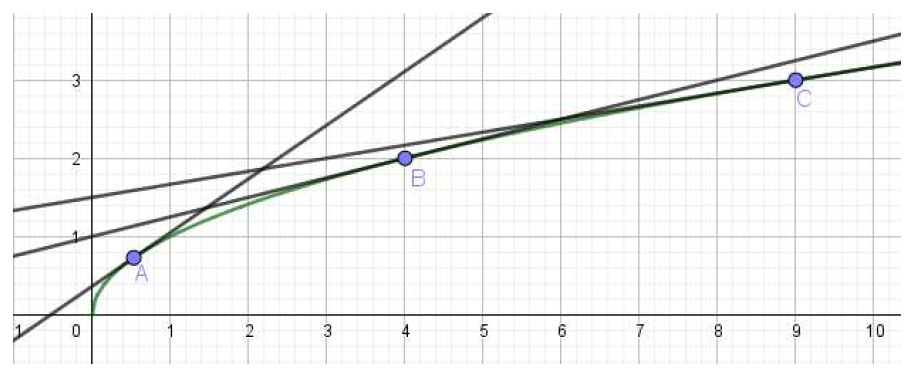
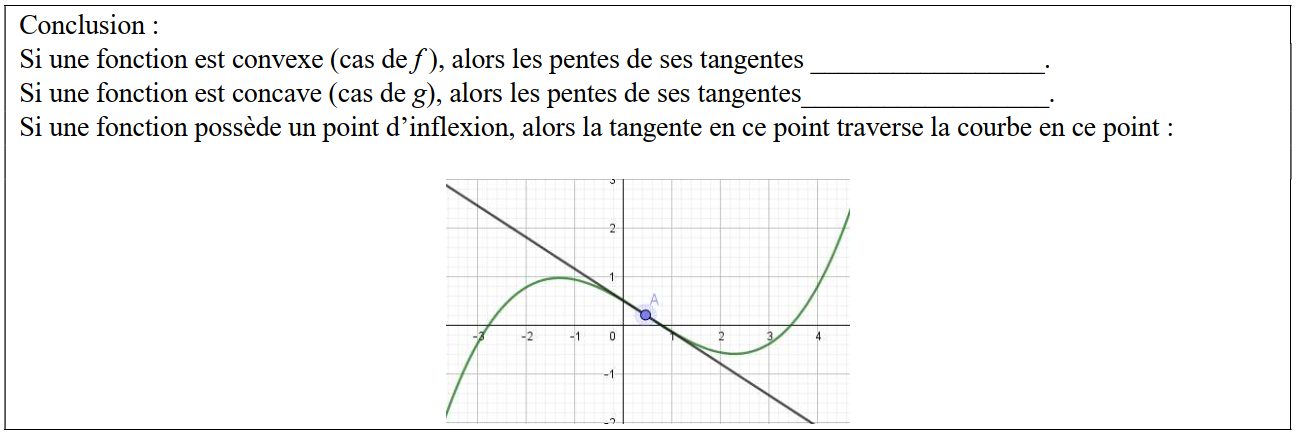

Pour visualiser cette conclusion, flasher le code ci-contre :
https://youtu.be/6SMG4o2EoGY
Théorème 1
Soit f une fonction définie et dérivable sur un intervalle I. Alors :
- f convexe sur I équivaut à f ’ croissante sur I
- f concave sur I équivaut à f ’ décroissante sur I
- la courbe représentative de f possède un point d’inflexion au point d’abscisse a équivaut à f ’ change de variation en a
A faire vous-même 5
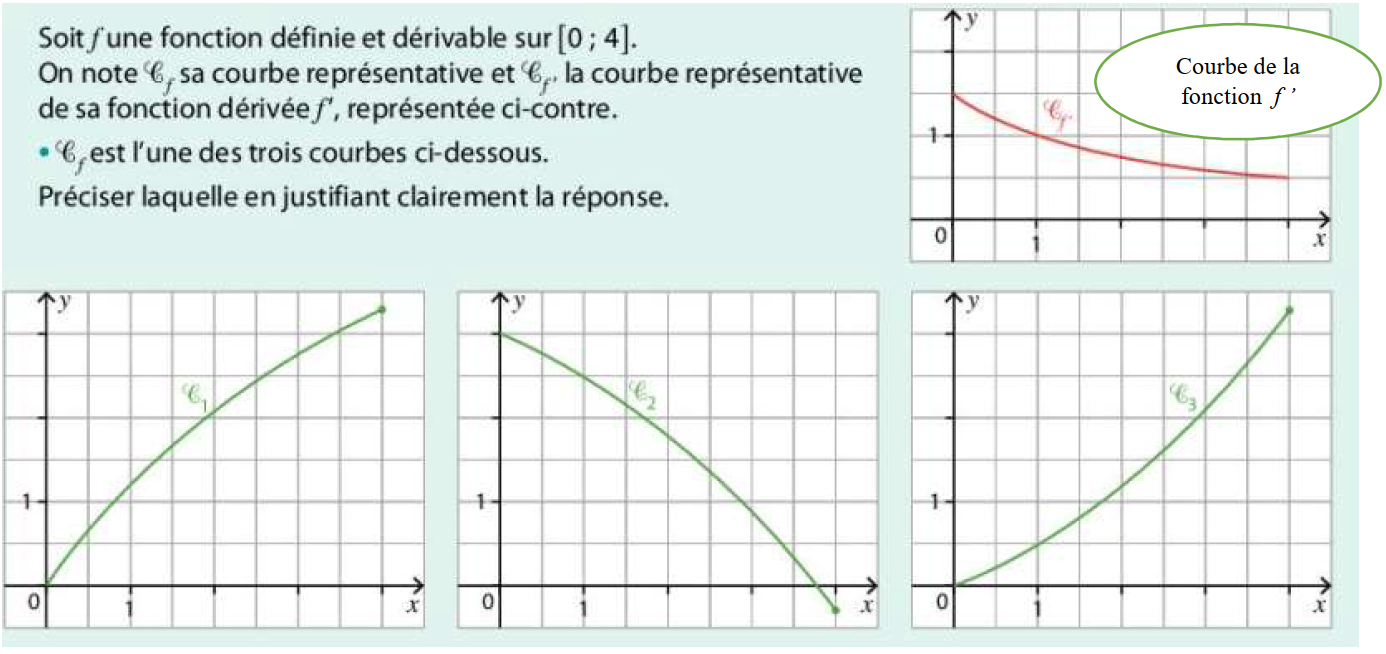
Nous venons donc de voir que pour étudier la convexité d’une fonction f, il fallait étudier les variations de la fonction f ’. Or nous savons que pour étudier les variations d’une fonction, il faut étudier le signe de sa fonction dérivée (cours de première). Il s’agit donc ici de déterminer la fonction dérivée de la fonction f ’, notée f ’’ et appelée dérivée seconde de la fonction f , et d’en déterminer son signe.
Théorème 2
Soit f une fonction définie et deux fois dérivable sur un intervalle I. Alors :
- f convexe sur I équivaut à f ’’positive sur I
- f concave sur I équivaut à f ’’ négative sur I
- la courbe représentative de f possède un point d’inflexion au point d’abscisse a équivaut à f ’’ s’annule et change de signe en a
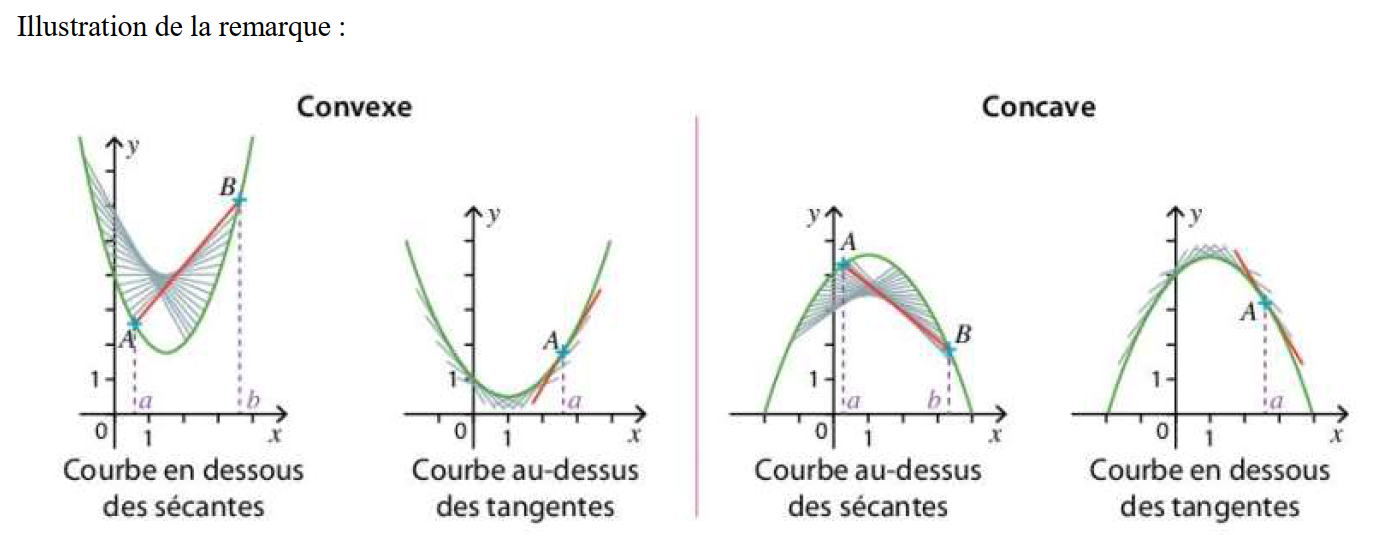
Si f est convexe sur I, alors sa courbe représentative est au-dessus de ses tangentes et en-dessous de ses sécantes sur I, et réciproquement.
Si f est concave sur I, alors sa courbe représentative est en-dessous de ses tangentes et au-dessus de ses sécantes sur I, et réciproquement.
Si f est concave sur I, alors sa courbe représentative est en-dessous de ses tangentes et au-dessus de ses sécantes sur I, et réciproquement.
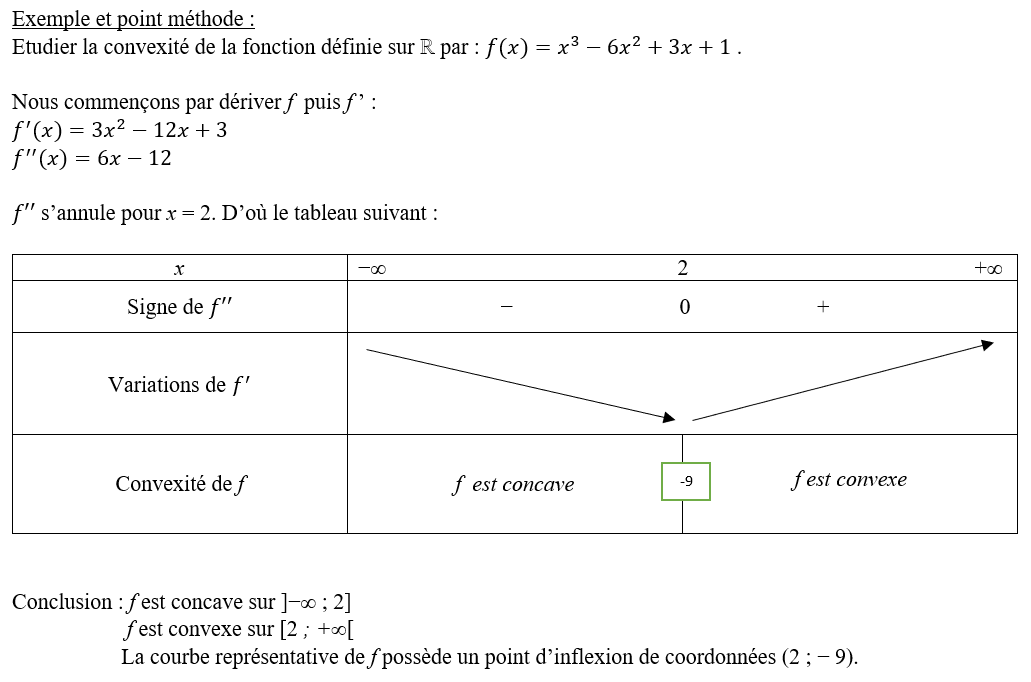
A faire vous-même 6
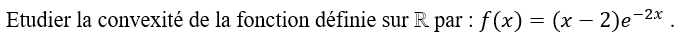
auteurs :
Labomaths Jean-Emmanuel Faucher, lycée Auguste et Jean Renoir, Angers
Mots clés :
Information(s) pédagogique(s)
Niveau :
tous niveaux, Terminale
Public visé :
non précisé

