Et si on évaluait l'algoritmique en devoir maison ? Comme support les nombres relatifs.
Contexte
Les élèves ont eu deux séances en salle informatique pour découvrir le logiciel Scratch.
La première séance a permis de tracer des quadrilatères, sans utiliser de boucle.
La deuxième séance les a amenés à tracer des quadrilatères et des triangles, en utilisant une boucle à chaque fois que cela était possible.
Le travail en classe est mené sur les nombres relatifs. Les élèves ont connaissance de l’addition et de la soustraction de deux nombres relatifs et débute à ce titre sur la notion d’opposé d’un nombre relatif.
Devoir maison n°1
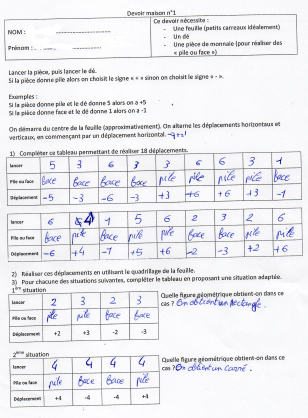
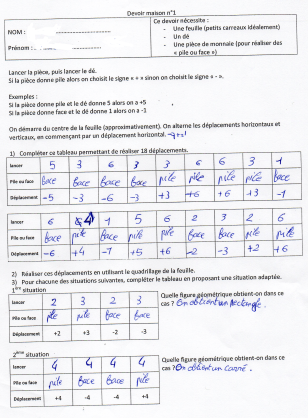
Le devoir maison n°1 est alors donné. ...
Ce devoir permet d’aborder et de consolider plusieurs notions :
Les nombres relatifs
Le déplacement dans le plan
Une première approche du hasard : le lancer d’un dé ou d’une pièce de monnaie a d’ailleurs fait l’objet d’une explication en classe afin de mettre en évidence la nécessité de bien respecter un protocole.
Les élèves ont un délai d’une semaine pour réaliser ce devoir.
Travaux d'élèves. ...
On peut remarquer sur l’énoncé un rappel de la convention « + : droite, haut et - : gauche, bas »
On peut observer une petite erreur dans la construction du chemin mais le principe est clairement acquis. Un sens de parcours est précisé.
Une imprécision dans une valeur numérique sur l’un des tableaux mais les figures géométriques associées sont bien visualisées. Il n’y a pas eu de tracés rendus pour cette question.
Le sens de parcours n’est pas précisé. Pour la dernière partie, la réponse s’appuie sur des figures tracées.
On retrouve ici un rappel de la convention de déplacement. Un code couleur sur les différents lancers permet à l’élève de s’y retrouver.
Le parcours précise le point de départ et le point d’arrivée ainsi que le sens du trajet.
TP informatique sur Scratch
a) Travail commun à tous Les élèves récupèrent alors leurs copies, qui sont majoritairement excellentes, et doivent travailler sur le TP n°3.
Le travail mené pendant la séance consiste principalement à décomposer ce qu’il y a à faire de façon à avancer de manière progressive. Peu à peu se mettent en place :
La simulation du pile ou face :
Le test si :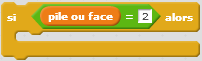
Le passage à l’opposé :
Lorsque tout cela est clair, il s’agit de concevoir le déplacement horizontal (donc « en x ») et le déplacement vertical (donc « en y »). Un groupement ‘de base’ est donc dupliqué :
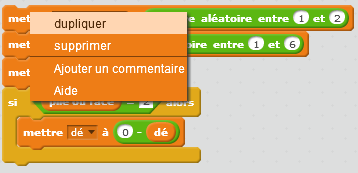
Il reste à associer les déplacements :
et
Pour respecter le fonctionnement du devoir maison, on intègre tout cela dans une boucle « répéter … fois »
b) Pour les plus rapides Les plus rapides ont ajouté une répétition du type « Répéter indéfiniment » :
Une première étape a consisté à juste ajouter le bloc Répéter indéfiniment :
Cela donne un visuel peu agréable parce que : - Le lutin peut redémarrer de n’importe où, par exemple un bord - Les marches aléatoires s’enchainent trop rapidement.
Une deuxième version a permis de corriger les éléments qui ne convenaient pas :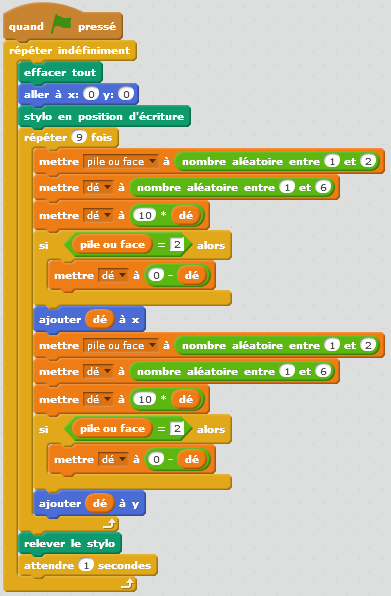
Cette version prévoir un retour au centre de la scène ainsi qu’une temporisation avec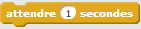
c) Une ouverture possible Cette ouverture n’a pas été traitée en classe : le passage du papier au logiciel nécessite de multiplier le déplacement par 10. On peut proposer un travailler où ce coefficient soit demandé à l’utilisateur de façon à visualiser à partir de quelle valeur le chemin sort régulièrement de la scène.
Devoir maison n°2
En prolongement de ce travail, le devoir maison n°2 permet un travail sur les nombres relatifs ainsi que sur les connaissances acquises sur Scratch. L’objectif ici est double : - Montrer une compréhension d’un algorithme simple ‘sur papier’ - Réinvestir les notions abordées sur les nombres relatifs.
Le devoir maison n°2. ...
Voici les éléments d’un programme avec le logiciel Scratch.
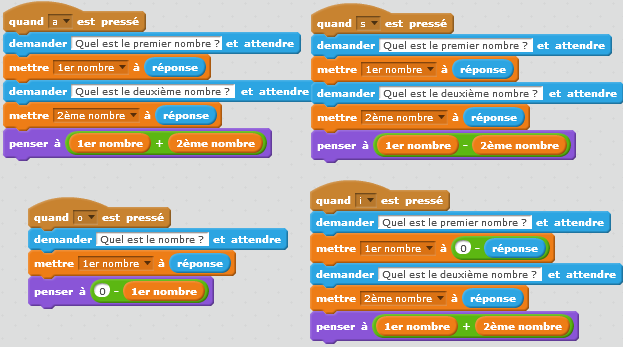
1ère partie :
1)Décrire ce qu’il se passe lorsque l’utilisateur appuie sur « a ». 2)Décrire ce qu’il se passe lorsque l’utilisateur appuie sur « s ». 3)Décrire ce qu’il se passe lorsque l’utilisateur appuie sur « o ». 4)Décrire ce qu’il se passe lorsque l’utilisateur appuie sur « i ».
2ème partie :
Image 1
Pour chacune des deux images ci-contre, proposer des nombres qui conviennent pour que le chat pense à cette réponse lorsque l’utilisateur appuie : 1/ sur « a » 2/ sur « s » 3/ sur « o » 4/ sur « i »
Image 2
3ème partie :
On sait dans cette partie que le premier nombre est 12. 1/ Sur quelles touches l’utilisateur a-t-il pu appuyer ? 2/ Pour chacune des touches possibles, quel doit être le deuxième nombre si le chat pense à la réponse
a)5 b)-8 c)0
Ce que fait le programme avec ‘a’ (addition) ou ‘s’ (soustraction) est généralement bien compris par les élèves. Cela devient plus délicat lorsqu’il s’agit de nommer l’opposé par exemple, souvent perçu d’ailleurs en ce début d’année comme un nombre nécessairement négatif ! Ce travail donne bien accès aux représentations, y compris fausses ou partielles, des élèves.
Travaux des élèves. ...
Ici, le calcul de l’opposé n’est pas abordé !
Il y a en revanche un bon usage de l’exemple, à quelques parenthèses près.
On retrouve ici une vision pour le moins imprécise de la notion d’opposée.
Le vocabulaire vu en classe n’est pas intégré et cet élève explique fort bien mais assez longuement cette notion.
Le nombre opposé est quand même cité parfois !
Là encore, l’absence de vocabulaire oblige à trouver une autre façon de le dire : ici avec des exemples.
À la suite de ces travaux, un exercice portant sur des algorithmes avec Scratch a été proposé lors d’une évaluation.
L'évaluation ...
Exercice 1 : 1) Tracer un triangle équilatéral ABD de côté 5 cm. 2) Placer le point C tel que : ABCD est un parallélogramme. Expliquer la construction. 3) Bertille affirme que le parallélogramme ABCD est en fait un losange. A-t-elle raison ? Pourquoi ?
Exercice 2 : 1) Que va réaliser le chat lorsqu’on va faire fonctionner ce programme avec Scratch ? 2) Que va réaliser le chat lorsqu’on va faire fonctionner ce programme avec Scratch ?
Exercice 3 : Calculer A = 9 + 7 ; B = 9 – 7 ; C = -5 + 18 ; D = 14 + (-5) ; E = -12 – 4 ; F = -7 + 9 ; G = 17 – 20 ; H = -17 – 20
Exercice 4 : 1) Observer le tableau suivant :
Nombre de côtés
3
4
5
6
7
8
9
10
11
12
Nom du polygone
Pentagone
Hexagone
Heptagone
Octogone
Ennéagone
Décagone
Hendécagone
Dodécagone
a) Quel nom donne-t-on à un polygone ayant 3 côtés ? b) Quel nom donne-t-on à un polygone ayant 4 côtés ?
2) On considère la figure ci-dessous. <
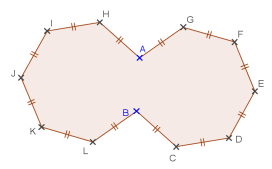
a) Quel nom peut-on donner au polygone AHIJKLBCDEFG ? b) Exprimer le périmètre de ce polygone ?
