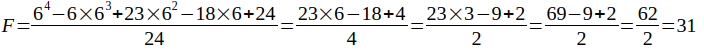- tous niveaux
- non précisé
secteurs de disque - une démonstration
Une démonstration liée à une expérimentation pédagogique sur le thème "favoriser l'esprit critique".
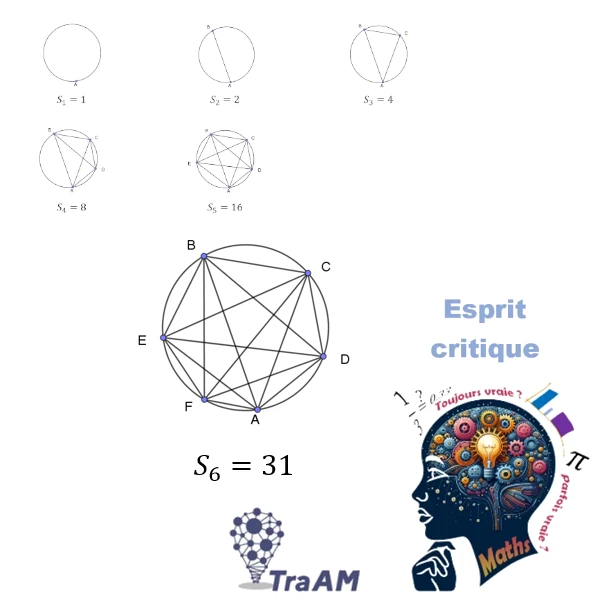
Un défi
Une poster est affiché dans les couloir du lycée afin que tout élève puisse y avoir accès et relever le défi.

Une proposition de correction
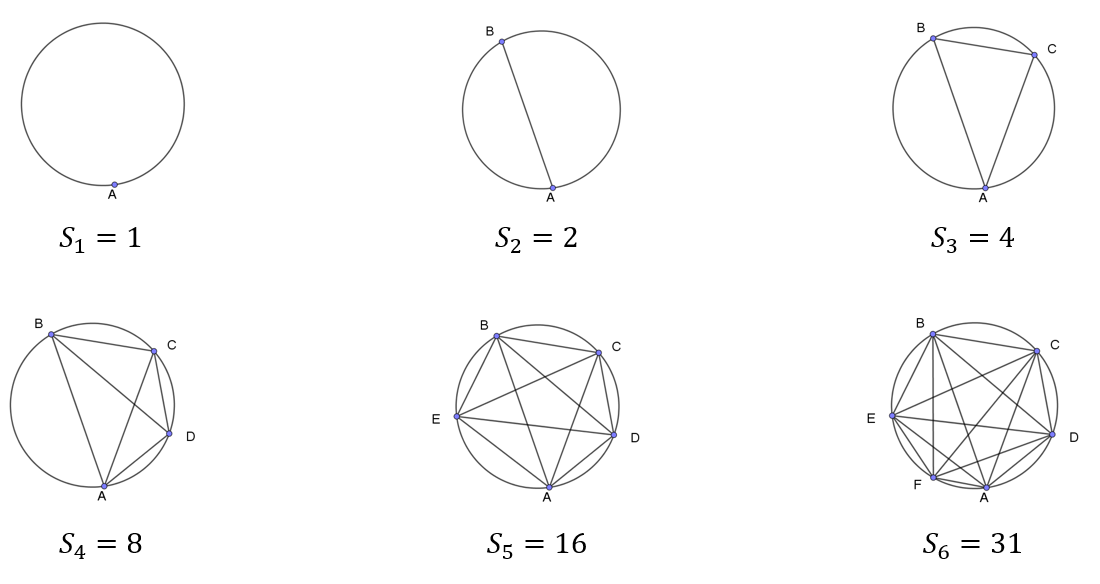
Eh non ! S6 n'est pas égal à 32...
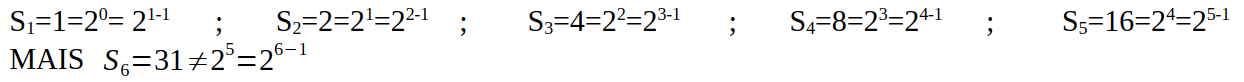
On aurait envie de conjecturer que Sn=2n-1 mais pour n=6 la formule devient fausse.
Démonstration
On commence par démontrer le lemme suivant dit d’Euler-Poincarré
Démonstration du lemme
On considère un polygone ayant n sommets. Le nombre d’arêtes les reliant est fini donc on peut trouver une droite du plan qui ne soit pas parallèle à une arête du polygone. Quitte à tourner le polygone, on peut choisir
cette droite de manière à ce qu’elle soit horizontale.
On va progressivement déplacer cette droite vers le bas, en gardant sa direction horizontale inchangée, du sommet supérieur du polygone au sommet inférieur.
Quelque soit sa position la droite ne pourra donc pas contenir plus d’un sommet du polygone.
Cette droite va nous servir à dénombrer A, le nombre d’Arêtes, F, le nombre de surFaces et S, le nombre de Sommets.
Dénombrons A, F et S en déplaçant la droite progressivement de haut en bas.
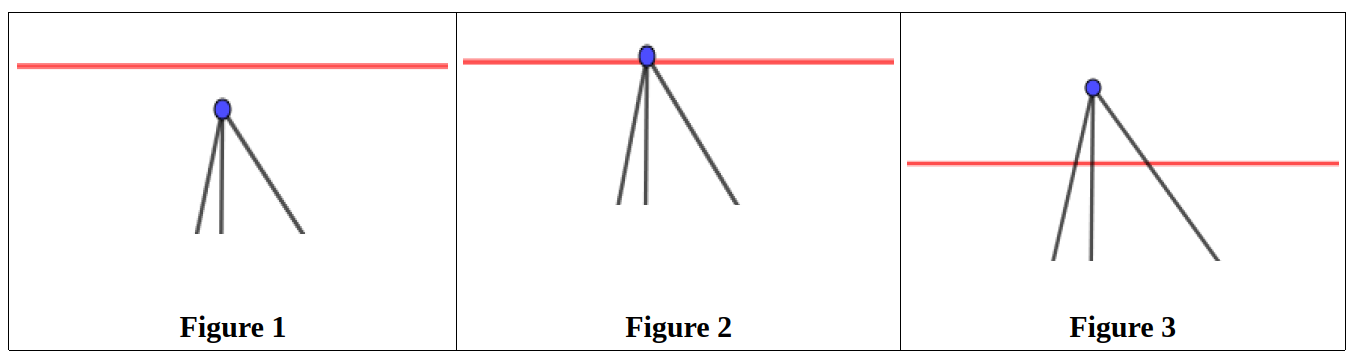
Quand la droite touche le sommet sans être entrée dans le polygone, la somme F– A+S vaut 1 car S=1, A=F=0.
En entrant depuis le sommet du haut dans le polygone, on a S=1. F, le nombre de surFaces est égal à A-1 car du sommet partent n arêtes et le sommet appartient à n-1 faces.
Donc la somme F– A+S=(A-1)-A+1=0.
Si on continue à faire descendre la « droite de coupe », on ne rencontrera qu’un seul sommet car l’on rappelle que c’est la condition que l’on a imposée lorsqu’on a choisit la direction de cette droite. Lorsqu’on rencontre un sommet dans cette descente, S, le nombre de sommets, s’incrémente de +1 et F-A se décrémente de 1.
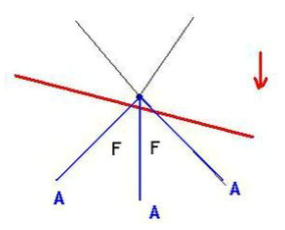
A chaque traversée de sommet, S gagne 1, (F-A) gagne -1. Ainsi S-A+F reste égal à 0.
Lorsque la droite traverse le dernier sommet (le plus bas) où il n’y a plus de faces et d’arêtes en dessous, S s’incrémente de 1 mais F-A ne varie pas puisque F et A ne le sont pas.
Ainsi, finalement, F-A+S=1
D’après le lemme, pour calculer le nombre de faces F du graphe il suffit de calculer A et S.
Calcul de S (nombre de surFaces)
Il y a deux types de sommets. Les sommets qui appartiennent au cercle et les sommets qui se trouvent à l’intérieur du cercle.
Le nombre de sommets qui se trouvent sur le cercle est égal à n.
Le nombre de sommets qui se trouvent à l’intérieur du cercle est égal à
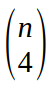
sommets parmi les n disponibles.
Ainsi
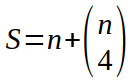
Calcul de A (nombre d’Arêtes)
Il y a trois types d’arêtes. Les arcs de cercle, les segments qui partent d’un sommet qui appartient au cercle et les segments qui partent d’un sommet qui se trouve à l’intérieur du cercle. On remarque qu’un de ces segments peut avoir pour extrémité un point du cercle et un point à l’intérieur du cercle.
Le nombre d’arc de cercle est égal à n.
Le nombre de segments qui partent d’un sommet qui appartient au cercle est égal à
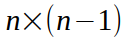
Le nombre de segments qui partent d’un sommet qui se trouve à l’intérieur du cercle est égale à
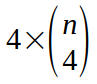
Dans le dénombrements précédent, les segments ont été comptés deux fois. Donc le nombre de segments est égal à
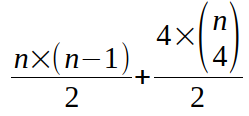
Ainsi, le nombre d’arêtes est égal à
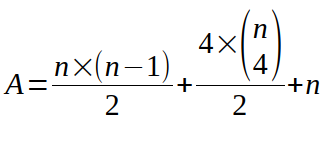
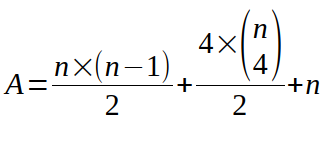
Calcul de F (le nombre de SurFaces)
Par suite, comme F=1+A-S, on en déduit que :
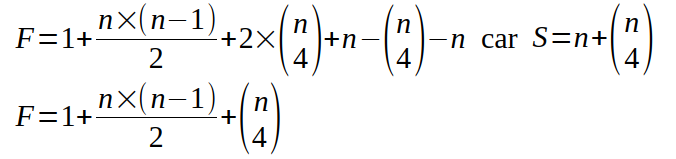
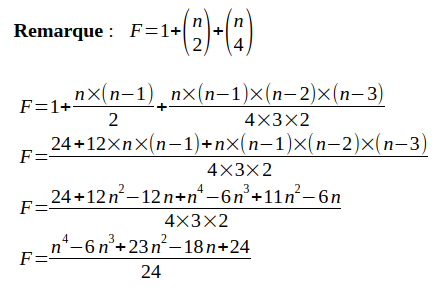
Pour n=6, le nombre de surFaces est égal à :