nombres décimaux : signification des chiffres - décompositions

Classe de CM2 (24 élèves)

Utiliser ses connaissances dans le domaine numérique pour résoudre un problème

• Déterminer la valeur de chacun des chiffres composant une écriture à virgule, en fonction de sa position
• Produire des décompositions liées à une écriture à virgule, en utilisant 10 ; 100 ; 1000.. et 0,1 ; 0,01 ; 0,001...

• utiliser à bon escient un tableur (calculatrice dans le texte officiel...) pour obtenir un résultat numérique issu d'un problème et interpréter le résultat obtenu.
• faire preuve d'esprit critique face à l'information et à son traitement

1. Travail sur tableur : demander aux élèves d'écrire 47,3 dans quatre cellules, une par signe comme ci-dessous :

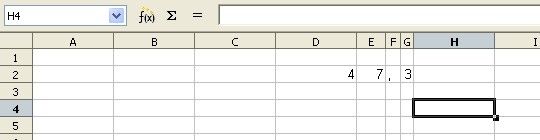
Poser la situation problème : "comment réécrire ce nombre dans une seule cellule, de façon à ce qu'il change si vous modifiez un ou tous les chiffres donnés au départ ?"

2. Laisser les élèves chercher la bonne formule. (lors des 2 séances précédentes, ils ont appris à écrire une formule avec des nombres entiers, en utilisant la syntaxe correcte : = ; nombres relatif, absolu, signes opératoires, parenthèses,...

cf. documents complémentaires : séquences / Construction du Nombre  -  Remédiation via l'outil tableur

Quelques erreurs fréquentes au départ :
Somme des cellules sans prise en compte de la valeur due à la position :

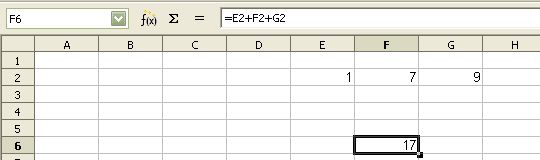
Insertion d'une valeur absolue parmi des valeurs relatives (nom de la cellule) : si l'on change le chiffre dans la cellule E2, le nombre d'arrivée ne changera pas.

3. Mise en commun des procédures utilisées ; les élèves viennent écrire leur formule au tableau, indiquent ce qu'ils obtiennent quand ils changent une des données de départ.
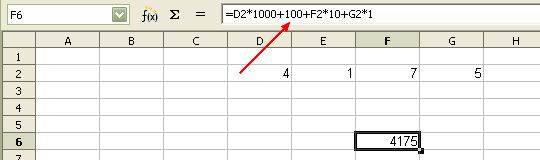
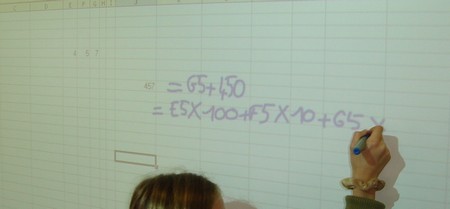
4. Phase de structuration : les formules qui fonctionnent sont réécrites au tableau :

5. Proposer un nouveau nombre, écrit sur 6 cellules : 405,67. Même démarche.
6. Quatre ou cinq nouveaux nombres au tableau ; les élèves doivent écrire deux décompositions différentes (types x 0,1 et /10) sur leur cahier du jour : le tableur ne servira qu'à vérifier les propositions.

• Ordinateurs, un pour deux élèves,
  Tableau Blanc Interactif éventuellement : facilite l'appropriation de la consigne et la mise en commun. Pas indispensable cependant.
• Tableur
  

Le tableur permet de créer une véritable situation problème ; pour les séances suivantes surtout : regroupement de deux ou trois chiffres sur une même cellule...

Le tableur permet une vérification immédiate des propositions des élèves ; s'ils se trompent dans la formule, les nombres de départ et d'arrivée ne seront pas identiques. Ils apprennent d'ailleurs rapidement à repérer le chiffre qui pose problème. Travail en relative autonomie une fois les problèmes "techniques" dépassés : les élèves rentrent dans la signification, la valeur des chiffres donc dans les notions mathématiques.

Le TBI permet de garder une trace des procédures, des formules. On peut y faire appel pour faire le lien entre des types d'erreurs. Il facilite aussi :
     l'appropriation du logiciel,
     la compréhension des consignes,
     les phases de mise en commun.

Séance riche pour apprendre à construire, reconstruire (décimaux) la notion de nombre. Les problèmes "techniques" liés à l'utilisation du tableur disparaissent très rapidement : l'outil sert alors les apprentissages.

• Motivation bien réelle : "on va trouver, attends un peu !!".
• Essais/erreurs : "on sait tout de suite si on a juste."
• Construction du nombre : "un nombre on peut l'écrire de plein de façons alors !"