Une résolution différente d’un problème similaire : on y jette un coup d'oeil ?
L’idée est tirée d’une correspondance historique entre Pierre de Fermat et Blaise Pascal. Les deux mathématiciens proposent une résolution différente d’un problème similaire (problème des parties) qu’on retrouve dès le XVe siècle dans des textes italiens. Deux amis jouent à un jeu équitable à plusieurs manches mais doivent se séparer avant la fin prévue. Comment répartir équitablement l’enjeu prévu. Ce problème marque le début des probabilités .
Sur le quai de la gare, deux amis jouent à un jeu de dés avec pour enjeu un paquet de 50 bonbons. Le jeu est simple, chacun lance un dé (à 6 faces) et celui qui obtient le meilleur score remporte une manche. En cas d’égalité, la manche est simplement annulée et on recommence un tour. Le premier arrivé à 3 manches gagnantes sera déclaré vainqueur de la partie.
Le jeu est vite lancé, mais à cause des égalités la partie s’allonge dans le temps et bientôt le train de Pierre rentre en gare et les deux amis doivent se séparer. A ce moment, Pierre a gagné deux manches et Blaise une seule.
Pierre déclare alors qu’il est le plus proche du but et doit donc être déclaré vainqueur. Blaise lui pense que la partie n’est pas terminé et qu’il faut donc partager le paquet de bonbons.
Comment trancher leur désaccord qui va bientôt animer le quai de la gare ?
Mise en place en classe
Avec une classe de première STI2D, l’activité est lancée 15min avant la fin du cours. Avec l’aide d’un volontaire (ici Liam), je joue la partie comme les deux protagonistes Pierre et Blaise. Arrivé à 2-1, je déclare qu’il est trop tard pour finir la partie et leur demande comment faire. Les deux premières propositions sont rapidement faites à l’oral par les élèves mais aussi écartées par des arguments simples. Je laisse la répartition en suspend et le cours suivant je reprends en écrivant au tableau les deux propositions (et leur contre argument), une troisième idée est apparue dans l’intervalle. Elle remporte l’approbation de l’ensemble de la classe.
Idée 1 : La partie était à l’origine équitable donc on sépare les gains entre les deux participants. Cela est injuste puisque Liam était plus proche de la victoire.
Idée 2 : Liam étant le plus proche de la victoire, il remporte tout. Cela est aussi injuste puisque le professeur pouvait encore gagner.
Idée 3 : Une répartition 2/3, 1/3 puisque Liam avait gagné 2 parties sur les 3 et le professeur 1 sur les 3.
Les élèves sont très contents de la troisième proposition qui est très simple et traduit bien l’idée que Liam était en avance. La question devient alors : Comment valider un choix de modélisation ?
Les élèves proposent d’essayer en classe pour voir : finir la partie une vingtaine de fois pour vérifier si leur proposition tient la route. On a donc ensemble essayé avec des dés puis créé un programme Python pour accélérer le processus (Un fichier Tableur est aussi possible)
Le résultat obtenu semble assez éloigné de la proposition initiale pour remettre en doute ce modèle
En version Tableur, cela donne par exemple :
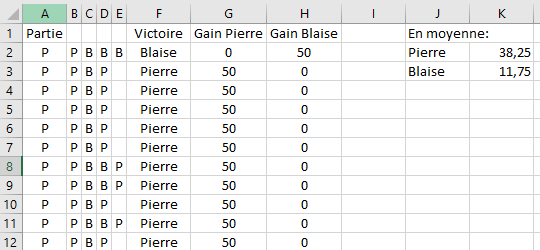
Je leur propose de tester la robustesse de leur modèle : Avec d’autres situations est-ce que le même raisonnement peut s’appliquer :
Et si la partie s’était arrêté à 1-1 ?
Et si la partie se jouait en 5 manches gagnantes ?
On se rend bien compte que leur modèle trop simple ne résiste pas à ce genre de questionnement.
Conclusion mis en avant
Une modélisation peut se valider ou s’invalider par la simulation et doit pouvoir être réutilisable lorsque les paramètres sont modifiés.
Quel que soit l’instrument choisi, on peut voir que le modèle communément choisi n’est pas représentatif de la réalité. Une fois admis cela, les élèves ont de nouveau réfléchi au problème et l’idée qui a émergé est proche de celle de Pierre de Fermat (voir plus loin) : Liam doit gagner une seule des deux parties suivantes alors que je devais gagner les deux.
Pour Pierre de Fermat : Il modélise le déroulement d’une partie par une suite de lettre. La lettre P symbolise la victoire de Pierre, et le B celle de Blaise. Le début de partie se note donc PPB. Il fait ensuite la liste des fins possible (il imagine une cinquième partie dans tous les cas même si elle s’avère inutile) : PPBBB, PPBBP, PPBPB et PPBPP. Il y donc 1 fin favorable à Blaise pour 3 fins favorable à Pierre. La répartition équitable sera donc 37,5 bonbons pour Pierre (3 quarts de 50) et 12,5 pour Blaise.
Pour Blaise Pascal : La partie prend la forme d’un schéma :
Il part ensuite des situations finales possibles pour trouver une répartition équitable. On notera les répartitions sous la forme d’un couple :
A l’étape 3 la répartition est (0 ;50) puisque Blaise gagne la partie
Aux étapes 1 et 2 la répartition est (50 ;0) puisque Pierre gagne la partie
L’étape marqué d’un A doit donc être une moyenne des étapes 2 et 3 puisque le jeu est équitable, on lui attribue donc le couple (25 ;25)
L’étape recherchée marquée d’un rond, est la moyenne des étapes A et 1 : (50+25) /2= 37,5 pour Pierre et (25+0)/2=12,5 pour Blaise
C’est le fait que les deux modèles donnent le même résultat qui renforce la confiance en celui-ci. Le modèle de Pierre de Fermat est facilement compris et ouvre la voie vers la notion d’espérance et celui de Blaise Pascal rappelle l’arbre et ouvre la voie vers les probabilités conditionnelles.
