Actions nationales 2019-2021
Voir le tableau synoptique des activités proposées
- Mieux cerner ce que l'on entend par Modéliser au travers d'exemples et des contre-exemples.
- Quelle mise en place en classe ? Une approche historique.
- Lien collège lycée : comment travailler la modélisation au collège pour commencer à construire des modèles au lycée ?


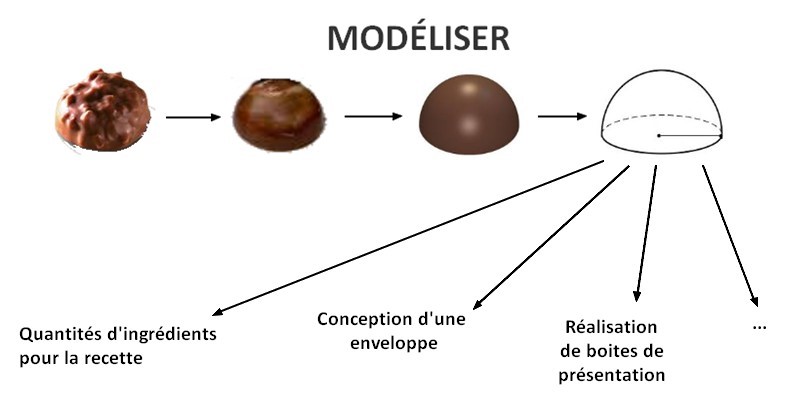
Le document sur la compétence commence ainsi :
" La compétence "Modéliser" , si on la prend dans son acception la plus large, renvoie pour le mathématicien au fait d’utiliser un ensemble de concepts, de méthodes, de théories mathématiques qui vont permettre de décrire, comprendre et prévoir l’évolution de phénomènes externes aux mathématiques."
Puis, un peu après, " La compétence "Modéliser" est, parmi les compétences travaillées, celle qui aborde de front le lien des mathématiques avec un extérieur à la discipline. "
Le groupe TraAM de l’Académie de Nantes a commencé à réfléchir à ce double passage
situation réelle


Une autre formulation, une autre approche est donc de s’intéresser à l’apport de l’abstraction sur une compréhension du réel.
Au collège particulièrement, une clé de l’entrée dans la modélisation est certainement la représentation. Représenter ouvre souvent la voie au calcul, au calcul pertinent.
Présentation jeu de l'oie
Focus sur " Modélisons une tasse à café "
Implicitement dans la présentation de l’exercice, la grande tasse est " indiquée " comme homothétique à la petite tasse que les élèves ont en main.
C’est une raison pour laquelle comparer la moyenne des résultats issus du modèle mathématique au résultat trouvé par la méthode de la physique et non l’inverse est probablement plus pertinent. Néanmoins, Si on regarde l’image de la grande tasse, ce n’est pas la réalité puisque le " renflement " à la base semble proportionnellement plus important pour la petite tasse que pour la grande…
Il convient alors de souligner la force du modèle mathématique et cette " force " vient justement de la simplification par un cylindre. Si la situation avait été travaillée au milieu du désert avec dans son sac à dos une photo du record et une tasse, le modèle mathématique effectué par les élèves aurait quand même permis de trouver l’ordre de grandeur (éventuellement sans règle gradué et on rejoint l’activité sur " mesurer avec ce que l’on a sous la main ").
Idem s’il avait été en classe au pôle sud…le froid aurait changer les conditions physiques (pression et température par exemple) mais la modélisation mathématique, elle, aurait permis de donner une réponse satisfaisante au problème posé.
Avec plus de temps, si on avait dit aux élèves, comment améliorer le modèle, la compréhension apportée par ce premier calcul, leur auraient-ils permis de dire : un grand cylindre au-dessus, un plus petit au-dessous et on refait les calculs ?
Conclusion et perspectives
Modéliser c’est comprendre un problème afin d’améliorer la réponse (si on avait le temps) et de voir les limites : radiateur à ailettes, tipi, voiture qui ressemble à des juxtapositions de parallélépipèdes, calculer le volume d’un cylindre par " rotation " d’un rectangle autour d’un axe (à rapprocher aussi de l’optimisation d’une canette)?
Cette compréhension est encore meilleure si on a des outils mathématiques adéquates (four solaire, tyrolienne dans le lycée, un terrain à aménager)
Lorsqu’un modèle est suffisamment satisfaisant, il peut devenir une théorie : les pavages proposés, dérivation, la datation au carbone 14.
Perspectives
Des exemples d'activités
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Surface de lac
Comment mettre en place une stratégie pour modéliser un lac ?
Ressource pédagogique Mis à jour le
-
La datation au carbone 14
Si on utilisait la datation au carbone 14 pour aller vers une nouvelle fonction ?
Ressource pédagogique Mis à jour le
-
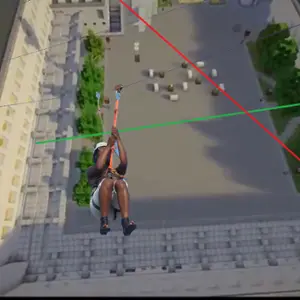
Le projet tyrolienne
Si on réalisait une tyrolienne pour l'installer dans la cour du lycée ?
Ressource pédagogique Mis à jour le
-
Le four solaire (une propriété de la parabole)
Lorsqu'on désire en faire plus avec des élèves de terminale qui se destinent à des études scientifiques.
Ressource pédagogique Mis à jour le
-
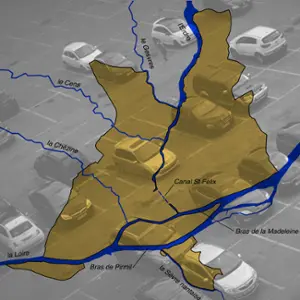
Se garer à Nantes
Pourquoi ne pas utiliser certaines données brutes, issues d’un « open data », afin de proposer un problème à modéliser.
Ressource pédagogique Mis à jour le
-
Un terrain à aménager
Que faire à partir du plan d’une parcelle qu’on obtient dès qu’on achète un domicile ?
Ressource pédagogique Mis à jour le
-
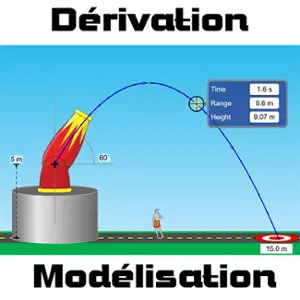
Une mise en place de la dérivation à partir d’un problème de modélisation
La dérivation est au cœur des notions à voir en analyse en classe de première que ce soit en première générale ou en première technologique : alors GO !
Ressource pédagogique Mis à jour le
-
Problème d’allées dans un jardin
Remobiliser le travail de modélisation algébrique effectué en 2de, travailler la résolution des équations du second degré nouvellement découverte.
Ressource pédagogique Mis à jour le
-
-
-
-
-
-
-
-
-
-
-
Des exemples d'activités incluant des plus anciennes pour lesquelles il y a modélisation, ou adaptables pour la modélisation
-
-
-
-
-
-
-
-
Faire des maths pendant les JO d’hiver de Pyeongchang 2018
10 exercices pour travailler les attendus de mathématiques du cycle 4 en suivant l’actualité sportive (volume 2)
Ressource pédagogique Mis à jour le
-
La tour Eiffel est-elle plus légère que l'air ?
La tour Eiffel plus légère que l'air ? Serez-vous curieux en allant plus loin ?
Ressource pédagogique Mis à jour le
-
200 litres
L’objectif de la séance est d’amener les élèves à avoir un regard mathématique sur une situation du quotidien.
Ressource pédagogique Mis à jour le
-
Faire des maths pendant les JO d’hiver de SOTCHI 2014
Et si les jeux olympiques nous permettaient d'aborder la géométrie, le calcul, la gestion de données et de manipuler les grandeurs et mesures.
Ressource pédagogique Mis à jour le
-
Empilements de boules
Cette activité permet au élève de s'approprier la modélisation du problème rapidement identifié comme une situation nécessitant des suites.
Ressource pédagogique Mis à jour le
-
La pyramide
Cette activité permet au élève de s'approprier la modélisation du problème rapidement identifié comme une situation nécessitant des suites.
Ressource pédagogique Mis à jour le
-
-