A partir d'une curiosité arithmétique, il s'agit de découvrir une formule algébrique. Dans la deuxième situation, plus difficile, le passage au calcul littéral, préparé par l'utilisation d'un tableur, est bien accompagné par l'utilisation du calcul formel.
Enoncé de l'activité
Première situation
Calculer :
Qu'y a-t-il de remarquable ? En est-il toujours ainsi ?
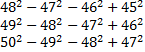
Deuxième situation
Vérifier que :
Qu'y a-t-il de remarquable ? En est-il toujours ainsi ?
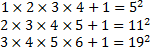
Déroulement du scénario
Première situation
Très rapidement, les élèves ont observé que chaque calcul avait pour résultat 4. Ensuite la plupart des élèves ont testé d'autres valeurs à la main puis au tableur et se contentent de l'expérimentation au tableur pour conclure. Peu d'élèves voient la nécessité de passer du tableur au calcul algébrique. Ils arrivent plus ou moins rapidement à une expression algébrique et le développement de cette expression se fait sans problème.
Deuxième situation
Pour la deuxième situation, les élèves ont d'abord mobilisé un tableur pour constater qu'effectivement, le nombre
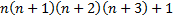
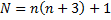
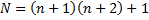
Le tableur confirme ce résultat qui reste à prouver.
Pour la preuve, les élèves commencent par développer l'expression
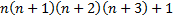
Ils doivent ensuite développer
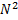
Le calcul formel permet le calcul accompagné par ordinateur et son utilisation confiance aux élèves.
Certains élèves ont directement tenté de factoriser l'expression :
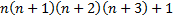
Avec l'accompagnement du professeur , ils ont piloté XCAS comme suit et sont venus expliquer leur résultat à la classe via le vidéoprojecteur.
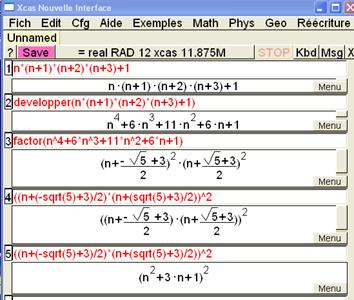
Les élèves sont d'abord surpris par la complexité de l'expression, les radicaux font peur mais le professeur rassure. D'autres radicaux ont déjà été rencontrés en factorisant :
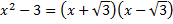
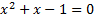
Ensuite, la discussion a été particulièrement intéressante pour le passage de l'étape 3 à l'étape 4. La propriété
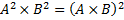
Enfin apparaît le carré d'un entier mais est-ce bien le même :
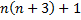
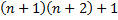
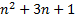
A-t-on bien , pour tout entier naturel n,
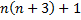
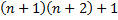
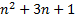
On le vérifie à la main et pas avec Xcas.
Le calcul formel permet à l'élève de passer aux commandes, il pilote et... il adore. L'élève identifie les calculs à faire, il décide de la stratégie à suivre et il délègue la tâche calculatoire au logiciel. Il confie au calculateur un calcul dont il maîtrise la nature mais dont il ne maîtrise pas la difficulté.
Compétences expérimentales
Prendre l'initiative d'utiliser un tableur pour tester la robustesse d'une conjecture.
Mobiliser un logiciel de calcul formel pour accompagner un calcul long, délicat ou inhabituel.
Piloter un logiciel de calcul formel après avoir identifié le besoin de calcul et la stratégie à suivre.
et