Quand la coupe du monde de rugby est un prétexte pour faire des mathématiques.
Préambule
La 9ème coupe du monde de Rugby se déroule au Japon du 20 septembre au 2 novembre 2019
Les 20 équipes qualifiées pour le tournoi sont réparties en 4 poules de 5 équipes. Chaque équipe dispute un match contre les 4 autres équipes de sa poule. A l'issue de ces 4 matchs, on établit un classement pour chaque poule avec le barème suivant :
Victoire : 4 points
Match nul : 2 points
Défaite : 0 point
Bonus offensif : 4 essais ou plus marqués lors d'un match : 1 point
Bonus défensif : défaite par 7 points ou moins lors d'un match : 1 point
Rappel des règles d’un match de rugby : lors d’un match, on peut marquer un « essai non transformé » pour 5 points, un « essai transformé » pour 7 points, une « pénalité ou un drop » pour 3 points. C’est l’équipe qui a le plus de points à la fin du match qui gagne.
1ère partie *: Pronostics des matchs de la poule C
Les professeurs de Rosamaths sont des spécialistes des paris sportifs. Voici leurs pronostics pour tous les matchs de la poule C (celle de la France) :
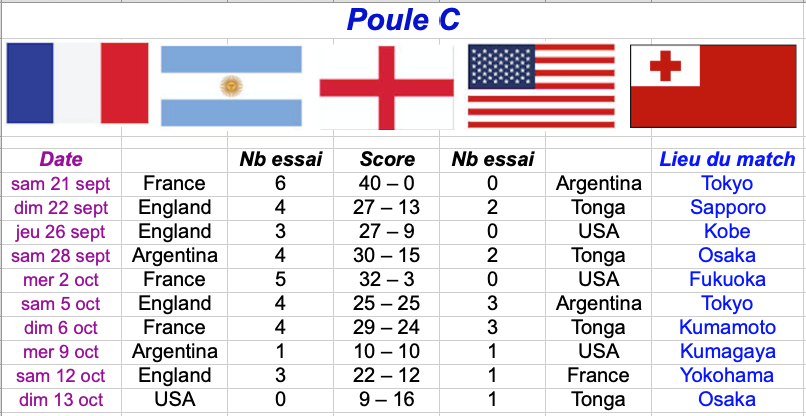
Q1) Avec ces pronostics, construire un tableau du classement de la poule C. Q2) Un des pronostics de ce tableau n'est pas possible. Lequel ? Pourquoi ? Q3) Dans une autre poule, un grand match opposera deux favoris : la Nouvelle-Zélande et l’Afrique du Sud.
Nous pensons que le score final sera de 23-19. Combien d’essais au minimum et au maximum pourront être marqués dans ce match ? Justifier
2ème partie ** : Marquer un essai
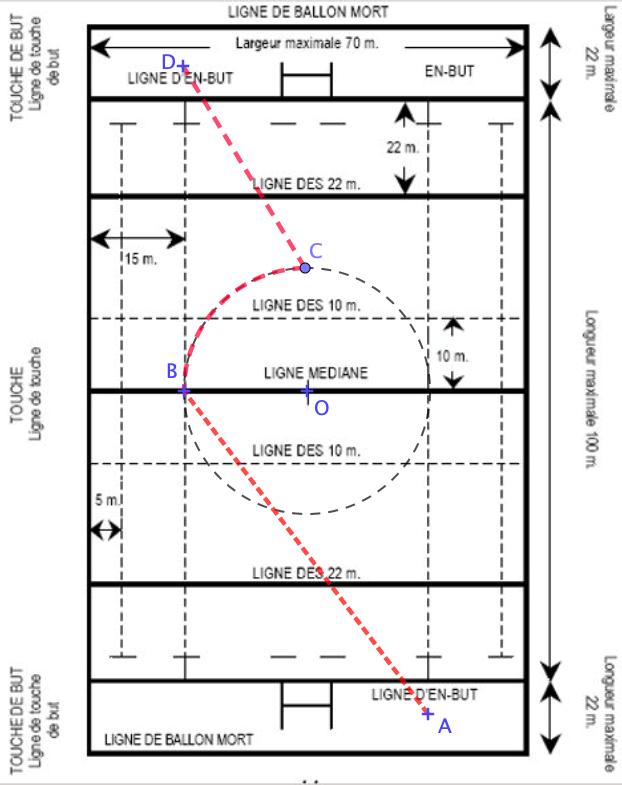Pour marquer un essai, une équipe doit aller aplatir, à la main, le ballon dans l’en-but d’averse. Elle marque alors 5 points.
Le jeune arrière Sergio est rapide. Il court à 30 km/h, part du point A, court en ligne droite vers le point B, puis fait un quart de cercle jusqu’à C avant de finir en ligne droite au D pour marquer un essai magnifique.
Q4) Combien de temps dure la course de Sergio ? (répondre au 1/100 de s près)
On précise : \(A\) et \(D\) sont situés 5 m derrière la ligne d’en-but et sont alignés avec les pointillés marquant les 15 m du bord de terrain.
3ème partie *** : Botter le ballon
Lorsqu’un adversaire a commis une faute ou lorsque son équipe a marqué un essai, le botteur peut tenter un coup de pied entre les poteaux (et au dessus d’une barre transversale située à \(3 m\) du sol). Considérons ici un botteur qui tente un coup de pied de pénalité d'un point situé à \(42,5 m\) des poteaux. Ce botteur est très adroit et sait qu’il va « viser droit » mais se demande si sa frappe sera assez puissante pour passer au dessus de la barre transversale… La trajectoire du ballon peut être modélisée par la fonction numérique \(h\) de la variable \(x\), définie sur l'intervalle [0 ; 45] par : \(h(x) = -0,03 x² + 1,35 x\) où \(x\) désigne la distance « horizontale » entre le pied du buteur et le ballon et \(h(x)\) exprime la hauteur du ballon par rapport au sol.
Q5) Représenter graphiquement (éventuellement à l’aide d’un logiciel) la fonction \(h\). Q6) Quelle est la hauteur maximale du ballon lors de sa trajectoire ? Remarque : les élèves de 2nde et de 1ère pourront répondre à l’aide du graphique. On attend des élèves de terminale une démarche par le calcul. Q7) La pénalité est-elle réussie ? Même remarque…
4ème partie **** : Transformer un essai (issu d’un sujet de bac S)
Lorsqu’un essai est marqué, l’équipe peut essayer de transformer cet essai pour 2 points supplémentaires : considérons qu’un essai a été marqué au point E (voir figure ci-dessous). La transformation consiste à taper le ballon par un coup de pied depuis un point \(T\) que le joueur a le droit de choisir n'importe où sur le segment \([EM]\) perpendiculaire à la droite \((AB)\). La transformation est réussie si le ballon passe entre les poteaux repérés par les points \(A\) et \(B\) sur la figure ci-dessous. On donne : \(EA = 25 m\) et \(AB = 5,6 m\)
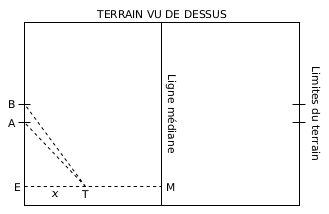
Q8) Imaginons que le botteur décide de placer le ballon en \(T\) tel que \(ET = 22 m\). Quel est dans ce cas la mesure de l'angle \(\widehat{ATB}\) ?
Pour maximiser ses chances de réussite, le botteur a intérêt à placer le ballon sur une position du point T qui rend l'angle \(\widehat{ATB}\) le plus grand possible. On cherche donc à déterminer à quelle distance ET (en m et au dm près), le botteur doit-il placer le ballon et quelle est alors la valeur de l’angle \(\widehat{ATB}\) (en degré à 0,1 degré près). A vous de jouer ! Toute démarche, toute stratégie de recherche est intéressante…
Le défi du mois : 30 joueurs de rugby mangent 30 kg de riz en 30 jours. Combien de riz mangent 15 joueurs de rugby en 15 jours ?
