problème d’allées dans un jardin

Le problème qui suit a été posé en activité flash à une classe de 1e Spécialité Maths.
Les objectifs étaient de remobiliser le travail de modélisation algébrique effectué en 2de et de travailler la résolution des équations du second degré nouvellement découverte.

Il s’agit d’un problème classique qu’on peut trouver dans les manuels de 2nde ou de 1ère sous diverses formes avec une figure déjà fournie. Le choix a été fait ici de ne donner que l’énoncé, sans figure, afin de travailler le processus de modélisation.

« Un jardin public a la forme d’un carré de 8 m de côté. Il est traversé par 2 allées perpendiculaires de même largeur. Ces deux allées ont une surface de 15 m² . Quelle est la largeur de l’allée ? »

L’un des premiers obstacles que vont rencontrer les élèves va être de correctement représenter l’énoncé. De cette représentation va découler une modélisation plus ou moins facile. Les deux sont étroitement liés.
Les élèves démarrent dans l’ensemble assez facilement le problème non sans leur rappeler de faire un schéma. Certains élèves ont cependant quelques difficultés qu’une lecture plus attentive de l’énoncé vient pallier.
Cependant, rapidement, plusieurs représentations apparaissent :

La configuration du milieu ainsi que celle de gauche, à des variantes de position près, sont les plus fréquentes.

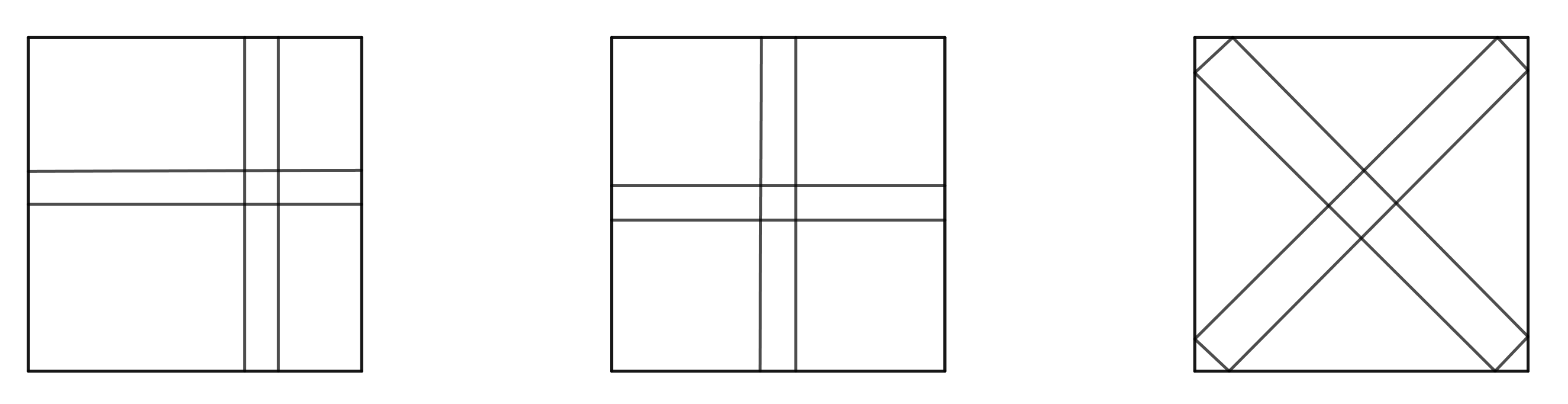
Quelques élèves font le schéma de droite, qui conduit à une autre modélisation et l’enseignant leur indique que cette possibilité est tout à fait juste mais trop difficile à traiter en l’état actuel. (Voir la fin du document pour une solution) Aucun élève ne pense à faire la représentation ci-contre :

Une fois les représentations trouvées par les élèves, ceux-ci doivent modéliser le problème.

Une moitié, en autonomie, modélise facilement en introduisant x comme la largeur de l’allée.
Une autre moitié n’y a pas recours et sont en difficulté pour poursuivre l’exercice, même après relance ou suggestion de passer par un intermédiaire d’essai-erreur.

La modélisation la plus courante rencontrée est celle qui consiste à calculer l’aire du carré et soustraire l’aire des allées. Cependant, aucun élève n’arrive à modéliser correctement l’équation car ils oublient que l’intersection des allées est comptée « deux fois ».

Après discussion et aide, les élèves modélisent le problème par l’équation suivante :


Ils résolvent ensuite l’équation.

Cependant, une autre élève, modélise différemment : elle calcule la surface restante dans le jardin une fois les allées enlevées. Avec un peu d’aide, elle arrive à la modélisation suivante :


Elle choisit de développer l’identité remarquable pour ensuite résoudre l’équation.

La synthèse est rapide et se passe en deux temps :

• Dans un premier temps, l’enseignant revient sur les représentations des élèves et le choix d’en écarter une. Il revient également sur les deux modélisations proposées et la méthode des résolutions d’une équation du second degré.
• Dans un deuxième temps, l’enseignant leur montre la dernière représentation (celle non envisagée par les élèves) et fait le lien avec une des modélisations rencontrées. Dans ce cas-là, il est possible de résoudre l’équation sans avoir recours au discriminant. La mise en évidence d’un choix de représentation, de son influence sur la modélisation et la difficulté qui en découle à résoudre le problème est mis en évidence.

Solution possible dans le cas des allées en diagonale

On pose $x$ la largeur de la diagonale. On a $0<x<8\sqrt{2}$ On doit donc déterminer sa longueur $NJ$ Etape 1 : On calcule la longueur $NC$ $NCO$ est un triangle rectangle isocèle en $C$. On pose $a=O=CN$ D’après le théorème de Pythagore $$\begin{gathered} O{N}^2=2a^2 \\ {x}^2=2a^2 \\ {a}^2=\frac{x^2}{2} \end{gathered}$$ d’où $a=\frac{x}{\sqrt{2}}=\frac{\sqrt{2}x}{2}$ car $x>0$ On en déduit $BN=8-\frac{\sqrt{2}x}{2}$

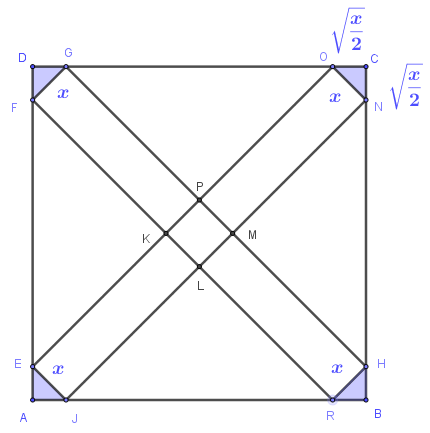$BNJ$ est un triangle rectangle isocèle.
D’après le théorème de Pythagore, on a :


$N{J}^2=B{J}^2+B{N}^2$
donc $N{J}^2=2{\left(\mathrm{(8}-\frac{\sqrt{2}x}{2}\right)}^2$)
d’où $NJ=\sqrt{2}\left|\mathrm{|8}-\frac{\sqrt{2}x}{2}\right||=\sqrt{2}\left(\mathrm{(8}-\frac{\sqrt{2}x}{2}\right)$ )
car $0<x<8\sqrt{2}$ donc $\frac{\sqrt{2}}{2}\times 0<\frac{\sqrt{2}}{2}\times x<\frac{\sqrt{2}}{2}\times 8\sqrt{2}$ donc $0<\frac{\sqrt{2}x}{2}<8$ donc $8>\frac{\sqrt{2}x}{2}>0$

On peut donc en déduire l’aire des deux allées.
On peut choisir, en fonction de l’énoncé, deux options :
Option A : Les triangles bleus font partie des allées
Option B : Les triangles bleus ne font pas partie des allées

Option A :
Option B :